Galois diagram
The previous post listed three posts I'd written before about images on the covers of math books. This post is about the image on the first edition of Dummit and Foote's Abstract Algebra.

Here's a version of the image on the cover I recreated using LaTeX.
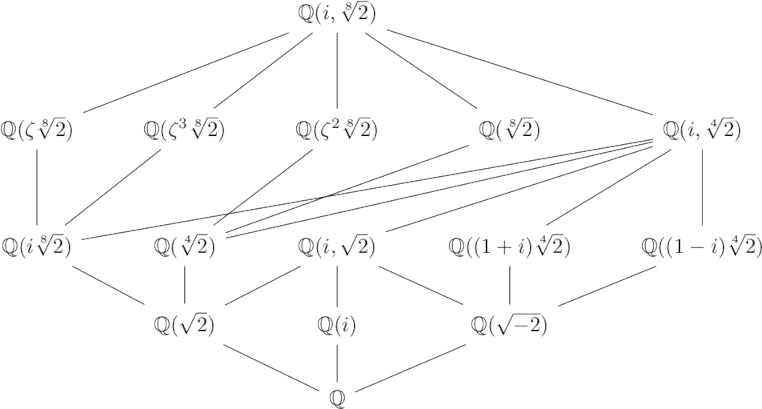
The image on the cover appears on page 495 and represents extension fields. If you're going through this book sequentially as a text book, it's likely time will run out before you ever find out what the image on the cover means. If you do get to it, you get to it near the end of your course.
My diagram is topologically equivalent to the original. I took the liberty of moving things around a bit to keep the diagram from being awkwardly wide.
At the bottom of the diagram we have , the field of rational numbers. At the top of the diagram we have (i, 21/8), the smallest field containing the rational numbers, the imaginary unit i, and the eighth root of 2. Lines between fields on two levels indicate that the higher is an extension of the lower. The constant in the diagram is
= i = 2(1 + i)/2.
The significance of the diagram is that extension field relationships like these are important in Galois theory. The image appears late in the book because the majority of the book is leading up to Galois theory.
The post Galois diagram first appeared on John D. Cook.