Which one is subharmonic?
The Laplace operator of a function of n variables is defined by
If f = 0 in some region , f is said to be harmonic on . In that case f takes on its maximum and minimum over at locations on the boundary of . Here is an example of a harmonic function over a square which clearly takes on its maximum on two sides of the boundary and its minimum on the other two sides.
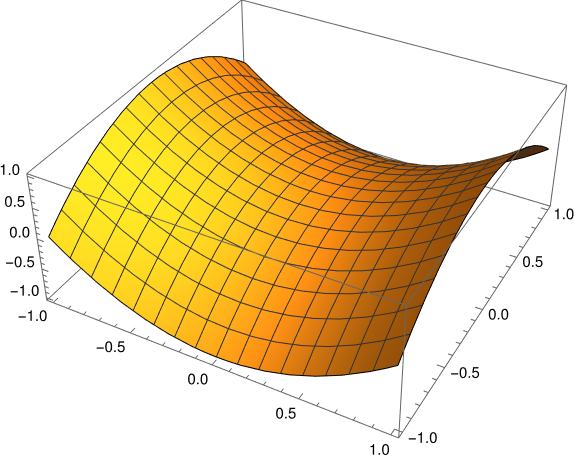
The theorem above can be split into two theorems and generalized:
If f >= 0, then f takes on its maximum on .
If f 0, then f takes on its minimum on .
These two theorems are called the maximum principle and minimum principle respectively.
Now just as functions with f equal to zero are called harmonic, functions with f non-negative or non-positive are called subharmonic and superharmonic. Or is it the other way around?
If f >= 0 in , then f is called subharmonic in . And if f 0 then f is called superharmonic. Equivalently, f is superharmonic if -f is subharmonic.
The names subharmonic and superharmonic may seem backward: the theorem with the greater than sign is for subharmonic functions, and the theorem with the less than sign is for superharmonic functions. Shouldn't the sub-thing be less than something and the super-thing greater?
Indeed they are, but you have to look f and not f. That's the key.
If a function f is subharmonic on , then f is below the harmonic function interpolating f from into the interior of . That is, if g satisfies Laplace's equation
then f g on .
For example, let f(x) = ||x|| and let be the unit ball in n. Then f >= 0 and so f is subharmonic. (The norm function f has a singularity at the origin, but this example can be made rigorous.) Now f is constantly 1 on the boundary of the ball, and the constant function 1 is the unique solution of Laplace's equation on the unit ball with such boundary condition, and clearly f is less than 1 on the interior of the ball.
Related posts- Laplacian in various coordinate systems
- Discrete harmonic functions
- Graph connectivity and Laplacian eigenvalues