Poisson distribution tail bounds

Yesterday Terence Tao published a blog post on bounds for the Poisson probability distribution. Specifically, he wrote about Bennett's inequalities and a refinement that he developed or at least made explicit. Tao writes

This observation is not difficult and is implicitly in the literature ... I was not able to find a clean version of this statement in the literature, so I am placing it here on my blog.

Bennett's inequalities say that for a Poisson random variable X with mean ,

for u >= 0 and

for -1 < u 0 where

I wanted to visualize how tight Bennett's bounds are and got some interesting images due to the discrete nature of the Poisson distribution.

Here's a plot of how tight the right-tail estimate is, the gap between the two sides of the first inequality above.

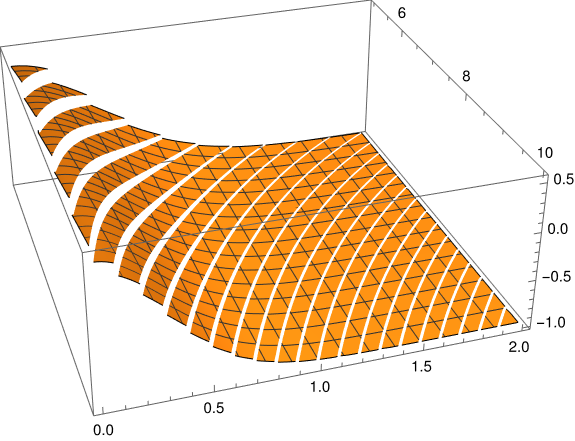
Here u ranges from 0 to 2 along the front edge of the graphic and ranges from 5 to 10.

And here's a plot of how tight the left-tail estimate is, the gap between the two sides of the second inequality above.

Mathematica tweaking

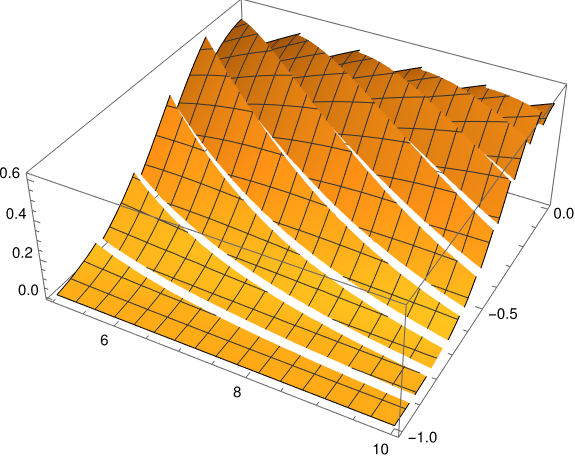
The latter image was easy to make, but the first image required a couple adjustments: the image had holes in it, and the view point was awkward.

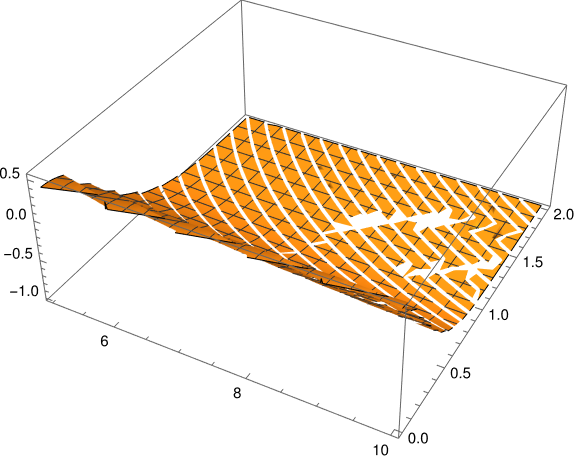
I fixed the holes in the plot by adding the option PlotPoints->50 to make the sampling finer. I fixed the view point by grabbing the image and rotating it until I thought it looked better. I could have saved the rotated image directly, but I was curious how to do this with the Export command. To do this I needed to specify the ViewPoint explicitly in the plotting command, but I didn't know how to get the value of ViewPoint that's I'd implicitly found via my mouse. A comment on the Mathematica Stack Exchange site told me what I needed to know.

Simply edit the output cell and wrap Options[..., ViewPoint] around the already rotated output. The graphics should be in the place of .... ViewVertical may also change during rotating, as well as some other parameters.

Related posts

• Upper and lower bounds on normal tails
• Improving on Chebyshev's inequality
• Statistics and data science consulting

The post Poisson distribution tail bounds first appeared on John D. Cook.