Pascal’s triangle mod row number

Almost all binomial coefficients are divisible by their row number.

This is a theorem from [1]. What does it mean?

If you iterate through Pascal's triangle, left-to-right and top-to-bottom, noting which entries C(m, k) are divisible by m, the proportion approaches 1 in the limit.

The author proves that the ratio converges to 1, but doesn't say anything about the rate at which it approaches 1. By writing a little Python script we can observe how the ratio approaches 1.

First, let's create a generator that will let us walk through Pascal's triangle.

 def pascal(): m, k = 0, 0 while True: yield (m, k) k += 1 if k > m: m += 1 k = 0

We can use this generator to illustrate Pascal's triangle mod row number.

 from math import comb p = pascal() m, k = next(p) while m 0 and comb(m, k) % m == 0: ch = "0" print(ch, end="") if m == k: print() m, k = next(p)

This produces the following.

 * 00 *0* *00* *0*0* *0000* *0***0* *000000* *0*0*0*0* *00*00*00*

The theorem says that as we keep going, the proportion of 0's in a diagram like the one above approaches 1.

Now let's plot the proportion of zeros as we traverse Pascal's triangle mod row number.

 N = 1000 x = np.zeros(N) p = pascal() for n in range(N): m, k = next(p) if m > 0 and comb(m, k) % m == 0: x[n] = 1 y = np.arange(N) plt.plot(y, x.cumsum()/y) plt.show()

Here's what we get.

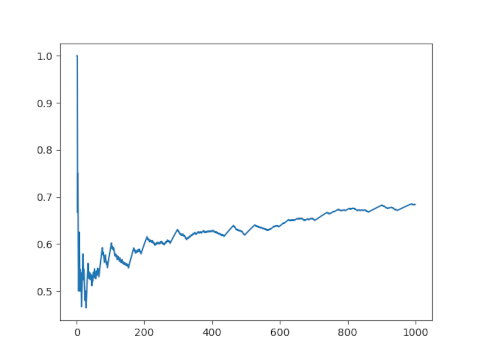
The ratio doesn't seem to be converging to 1. If I had to guess, I might say it's converging to 0.7 by looking at this plot. But if we go further out and switch to a log scale it seems more plausible that the sequence is converging to 1, albeit very slowly.

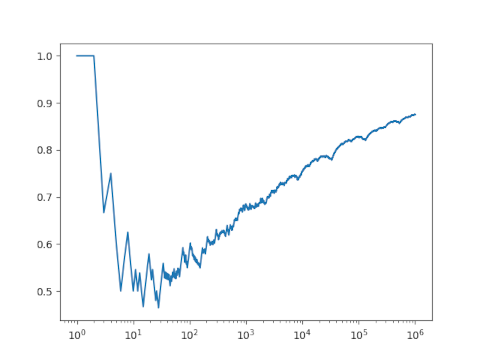
[1] Heiko Harborth. Divisibility of Binomial Coefficients by Their Row Number. The American Mathematical Monthly, Jan. 1977, Vol. 84, No. 1, pp. 35-37.

The post Pascal's triangle mod row number first appeared on John D. Cook.