Law of tangents
I would have thought that the laws of sines, cosines, and tangents were all about equally familiar, but apparently that is not the case. Here's a graph from Google's Ngram viewer comparing the frequencies of law of sines, law of cosines, and law of tangents.
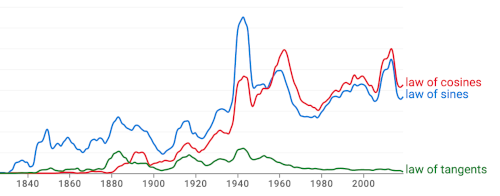
As of 2019, the number of references to the laws of sines and cosines are two orders of magnitude more than the number of references to law of tangents.
Law of tangentsSo what is the law of tangents?
Let a, b, and c be the lengths of the sides of a triangle and let , , and be the angles opposite a, b, and c respectively. Then the law of tangents says
We could make this equation more symmetric by multiplying the numerator and denominator on the left by . This extra factor of will be necessary shortly.
Note that on the left we have a ratio of distances and on the right we have a ratio of tangents of angles.
Law of tangents on a sphereNow let's imagine a triangle drawn on a sphere. Again we let a, b, and c be the lengths of the sides of a triangle and let , , and be the angles where the sides come together, the angle opposite a, opposite b, and opposite c.
The sides of the triangle are arcs, portions of great circles, and so the sides are also angles. The analog of the law of tangents in spherical trigonometry looks very much like the law of tangents above for the plane.
This form of the law of tangents is even more symmetric.
Because tan for small , the law of tangents on a sphere reduces to the law of tangents in the plane for small triangles, small relative to the radius of the sphere.
Update: See the next post on the law of cotangents.
Related postsThe post Law of tangents first appeared on John D. Cook.