Zeta sum vs zeta product
The Riemann zeta function (s) is given by an infinite sum and an infinite product
for complex numbers s with real part greater than 1 [*].
The infinite sum is equal to the infinite product, but which would give you more accuracy: N terms of the sum or N terms of the product? We'll take a look at this question empirically.
The accuracy of the partial sum and the partial product depends on N and on s. For starters, let's fix s = 3 and look at the approximation error as a function of N. Note that the error is plotted on a log scale.
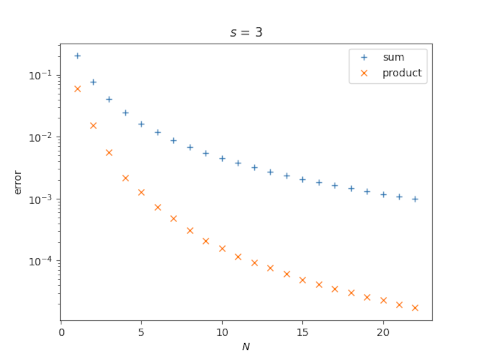
Now let's fix N = 10 and look at the error as a function of s.
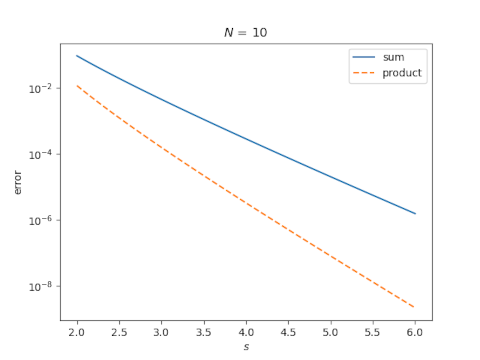
So our two examples suggest that taking N terms of the product gives more accuracy than taking N terms of the sum.
In the paper mentioned in the previous post, the author approximates the zeta function with a few terms of the product. That's what motivated this post. I thought the product might give more accuracy than the sum, and that appears to be the case.
Related posts[*] If you evaluate the series for at s = -1, despite the fact that the equation does not hold at that point, and evaluate at -1 using analytic continuation, you get the infamous nonsensical result that the positive integers sum to -1/12.
The post Zeta sum vs zeta product first appeared on John D. Cook.