Hénon’s dynamical system

This post will reproduce a three plots from a paper of Henon on dynamical systems from 1969 [1].

Let be a constant, and pick some starting point in the plane, (x₀, y₀), then update x and y according to

x_n+1 = x_n cos - (y_n - x_n^2) sin
y_n+1 = x_n sin + (y_n - x_n^2) cos

When I tried out Henon's system for random starting points, I didn't get plots that were as interesting as those in the original paper. Henon clearly did a lot of experiments to produce the plots chosen for his paper. Because his system is chaotic, small changes to the initial conditions can make enormous differences to the resulting plots.

Henon lists the starting points used for each plot, and the number of iterations for each. I imagine the number of iterations was chosen in order to stop when points wandered too far from the origin. Even so, I ran into some overflow problems.

I suspect the original calculations were carried out using single precision (32-bit) floating point numbers, while my calculations were carried out with double precision (64-bit) floating point numbers [2]. Since the system is chaotic, this minor difference in the least significant bits could make a difference.

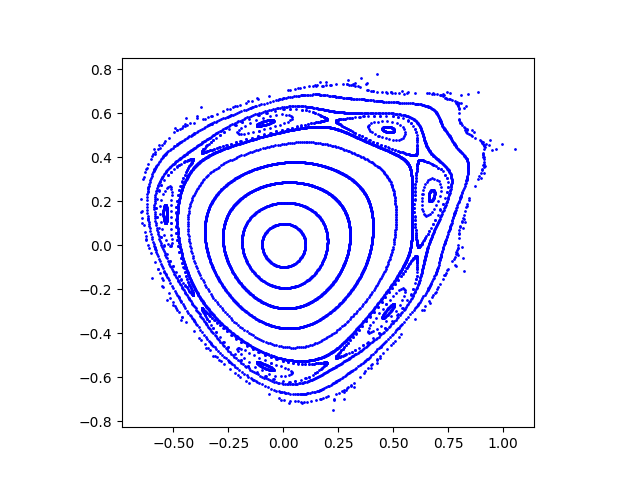
Here is my reproduction of Henon's Figure 4:

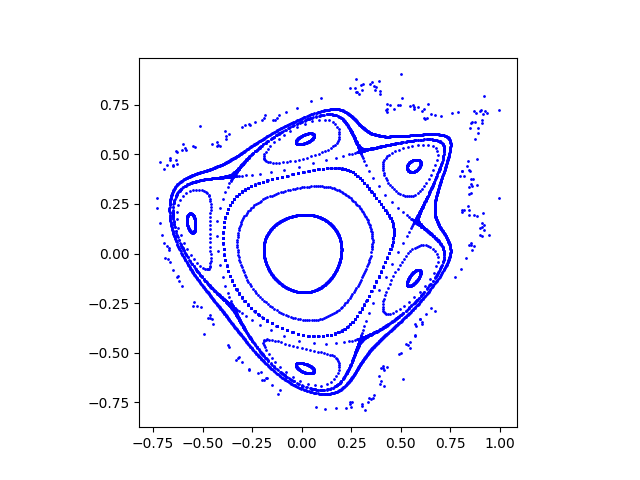
Here is my reproduction of Figure 5:

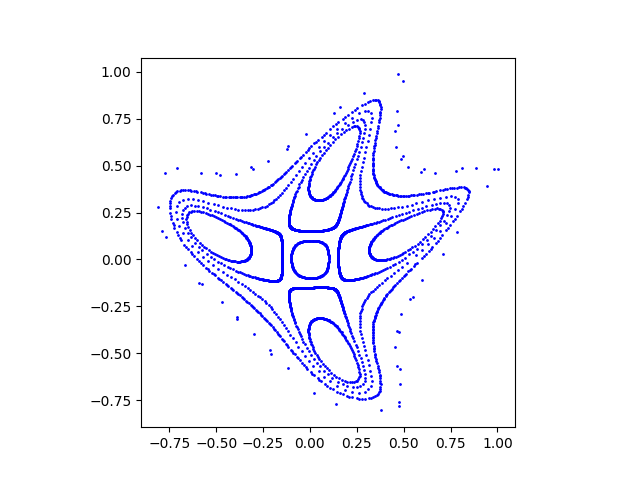
And finally Figure 7:

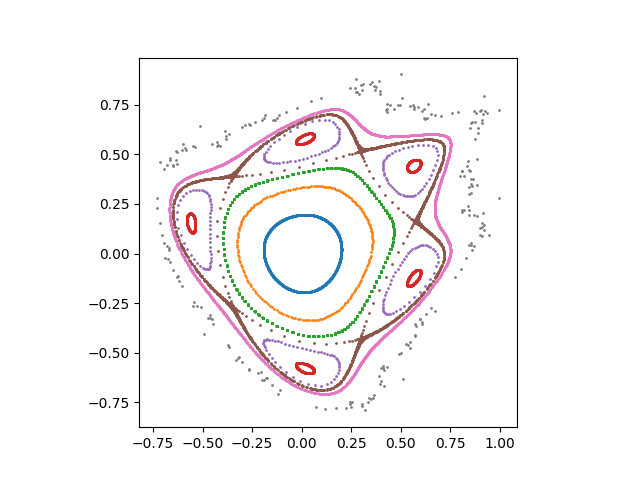
Update: You could use colors to distinguish the trajectories of different starting points. Here's a color version of Figure 5:

Related posts

For more posts like this, see Dynamical systems & chaos.

Python code

Here is the code that produced the plots. The data starting points and number of iterations were taken from Table 1 of [1].

import matplotlib.pyplot as plt# Henon's dynamical system# M. Henon. Numerical study of squadratic area-preserving mappings. Quarterly of Applied Mathematics. October 1969 pp. 291--312def makeplot(c, data): s = (1 - c*c)**0.5 for d in data: x, y, n = d for _ in range(n): if abs(x) < 1 and abs(y) < 1: x, y = x*c - (y - x**2)*s, x*s + (y - x**2)*c plt.scatter(x, y, s=1, color='b') plt.gca().set_aspect("equal") plt.show()fig4 = [ [0.1, 0, 200], [0.2, 0, 360], [0.3, 0, 840], [0.4, 0, 871], [0.5, 0, 327], [0.58, 0, 1164], [0.61, 0, 1000], [0.63, 0.2, 180], [0.66, 0.22, 500], [0.66, 0, 694], [0.73, 0, 681], [0.795, 0, 657],]makeplot(0.4, fig4)fig5 = [ [0.2, 0, 651], [0.35, 0, 187], [0.44, 0, 1000], [0.60, -0.1, 1000], [0.68, 0, 250], [0.718, 0, 3000], [0.75, 0, 1554], [0.82, 0, 233],]makeplot(0.24, fig5)fig7 = [ [0.1, 0, 182], [0.15, 0, 1500], [0.35, 0, 560], [0.54, 0, 210], [0.59, 0, 437], [0.68, 0, 157],]makeplot(-0.01, fig7, "fig7.png")

[1] Michel Henon. Numerical study of quadratic area-preserving mappings. Quarterly of Applied Mathematics. October 1969 pp. 291-312

[2] Single" and double" are historical artifacts. Double" is now ordinary, and single" is exceptional.

The post Henon's dynamical system first appeared on John D. Cook.