How Albrecht Dürer drew an 11-sided figure
You cannot exactly construct an 11-sided regular polygon (called a hendecagon or an undecagon) using only a straight edge and compass. Gauss fully classified which regular n-gons can be constructed, and this isn't one of them [1].
However, Albrecht Durer [2] came up with a good approximate construction for a hendecagon.
To construct an eleven-sided figure by means of a compass, I take a quarter of a circle's diameter, extend it by one eighth of its length, and use this for the construction of of the eleven-sided figure.
It took some trial and error for me to understand what Durer meant.
In more explicit terms, draw a circle of radius R centered at the origin. Then draw a circle of radius 9R/16 centered at (R, 0). Then draw a line from the origin to the intersection of the two circles. (There are two intersections, and it doesn't matter which one you pick.) Then this line makes an angle of approximately (360/11) degrees with the x-axis.
Without loss of generality we can assume R = 1. A point at the intersection of both circles satisfies the equation of each circle, and from these two equations in two unknowns we can determine that the x coordinate of the two intersection points is 431/512. We can then use the Pythagorean theorem to solve for y and find the inverse tangent of y/x. This shows that we've constructed an angle of 32.6696. We were after an angle of 32.7272, and so the relative error in Durer's approximation is less than 0.2%.
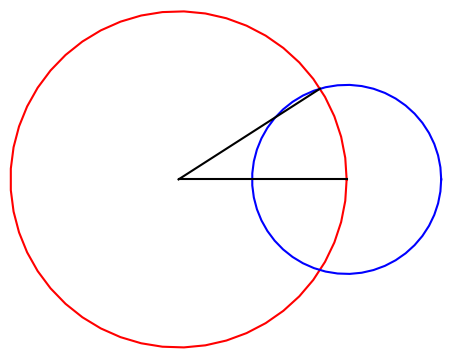
To be even more explicit, here is the Python code that created the image above.
import matplotlib.pyplot as plt from numpy import linspace, sin, cos, pi r = 9/16 t = linspace(0, 2*pi) plt.plot(cos(t), sin(t), 'r-') plt.plot(r*cos(t) + 1, r*sin(t), 'b-') x = 431/512 y = (1 - x*x)**0.5 plt.plot([0, 1], [0, 0], 'k') plt.plot([0, x], [0, y], 'k') plt.gca().set_aspect("equal") plt.axis("off") plt.savefig("durer11.png")More Durer posts[1] The Guass-Wantzel theorem says a regular n-gon can be constructed with straight edge and compass if n factors into a power of 2 and distinct Fermat primes.
[2] I found this in A Panoply of Polygons which in turn cites The Polygons of Albrecht Durer -1525" By Gordon Hughes, available on arXiv.
The post How Albrecht Durer drew an 11-sided figure first appeared on John D. Cook.