The essence of chaos
by John from John D. Cook on (#6B0PF)
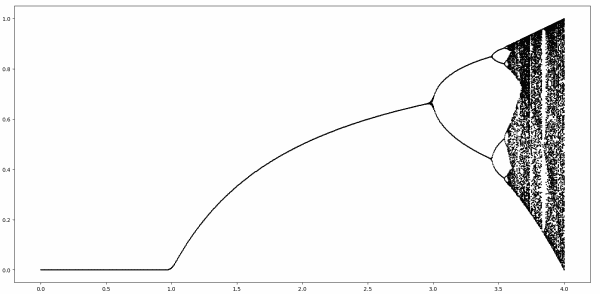
Linear systems can show sensitive dependence on initial conditions, but they cannot be chaotic. Only nonlinear systems can be chaotic.
George Datseris and Ulrich Parlitz explain this well in their book Nonlinear Dynamics:
Related postsThe post The essence of chaos first appeared on John D. Cook.... Sensitive dependence is not sufficient for a definition of chaos. ... the state space is first stretched and then folded within itself. This is the defining characteristic of chaotic systems. The stretching part is where sensitive dependence comes from ... as state space volumes increase in size ... nonlinear dynamics takes over and folds the state space back in on itself. ... This is why only nonlinear systems can be chaotic: linear systems with positive Lyapunov exponents always escape to infinity.