Trig crossings and root of gold
by John from John D. Cook on (#6C81Y)
Here's a curious fact. The graphs of cotangent and secant cross at the same height as the graphs of tangent and cosecant, and this common height is the square root of the golden ratio .
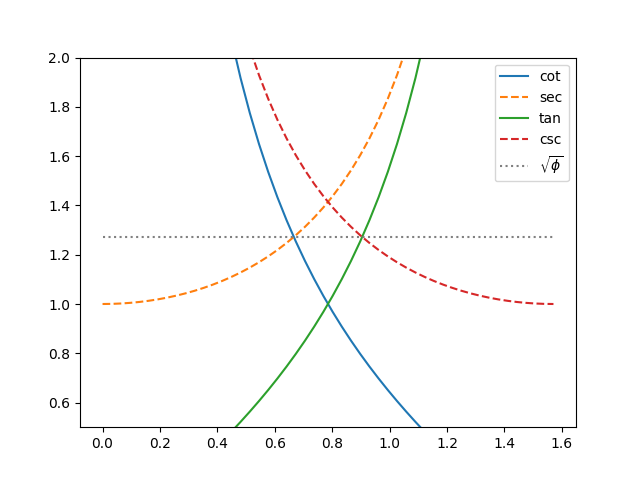
It's also the case that the graphs of hyperbolic cosecant and hyperbolic cosine, and the graphs of hyperbolic sine and hyperbolic cotangent, also cross at the same height, .
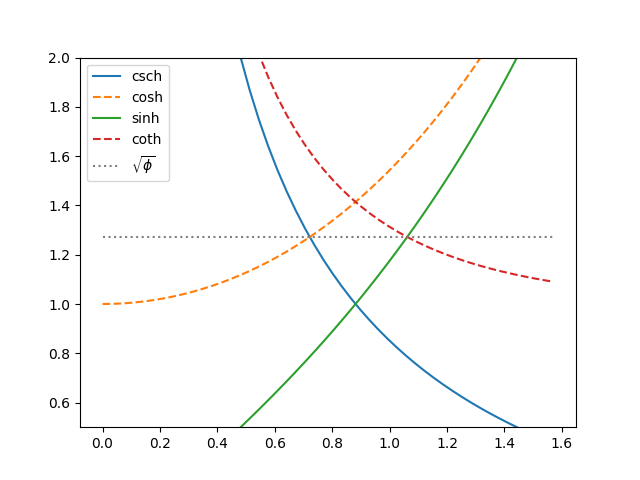
Source: P. J. Leah and J. B. Wilker. Hyperbolic and Trigonometric Crossing Points. Mathematics Magazine, Vol. 63, No. 3 (Jun., 1990), pp. 179-183
Related postsThe post Trig crossings and root of gold first appeared on John D. Cook.