A parabola, a triangle, and a circle
by John from John D. Cook on (#6C963)
Let P be a parabola. Draw tangents to P at three different points. These three lines intersect to form a triangle.
Theorem: The circumcircle of this triangle passes through the focus of P. [1]
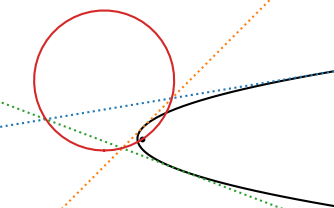
In the image above, the dashed lines are tangents and the black dot is the focus of the parabola.
(See this post for an explanation of what focus and directrix mean.)
By the way, creating the image above required finding the circle through the three intersection points. See the previous post for how to find such a circle.
[1] Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Mathematical Association of America. 1995. Page 47.
The post A parabola, a triangle, and a circle first appeared on John D. Cook.