Lehman’s inequality, circuits, and LaTeX
Let A, B, C, and D be positive numbers. Then Lehman's inequality says
This inequality can be proved analytically, but Lehman's proof is interesting because he uses electrical circuits [1].
Let A, B, C, and D be the resistances of resistors arranges as in the circuit on the left.
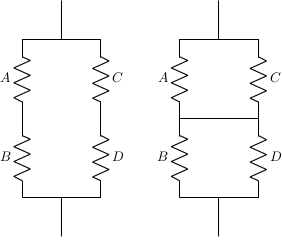
Resistors R1 and R2 in series have a combined resistance of
and the same resistors in parallel have a combined resistance of
This means the circuit on the left has combined resistance
The resistance of the circuit on the right is
Adding a short cannot increase resistance, so the resistance of the circuit on the right must be the same or lower than the resistance of the one on the left. Therefore
I drew the circuits above using the circuitikz package in LaTeX. Here's the code to draw the circuit on the left.
\documentclass{article} \usepackage{tikz} \usepackage{circuitikz} \begin{document} \begin{figure}[h!] \begin{center} \begin{circuitikz} \draw (0,0) to[R=$B$] (0,2) to[R=$A$] (0,4) to[short] (2,4) to[R=$C$] (2,2) to[R=$D$] (2,0) to[short] (0,0); \draw (1,4) to[short] (1, 5); \draw (1, 0) to[short] (1, -1); %\draw (0, 2) %to[short] (2, 2); \end{circuitikz} \end{center} \end{figure} \end{document}The code to draw the second circuit removes the %'s commenting out the code that draws the short between the two parallel arms of the circuit.
[1] Alfred Lehman proves a more general result using circuits in SIAM Review, Vol. 4, No. 2 (April 1962) pp. 150-151. Fazlollah Reza gives a purely mathematical proof on pages 151 and 152 of the same journal.
The post Lehman's inequality, circuits, and LaTeX first appeared on John D. Cook.