Newton’s inequality and log concave sequences

The previous post mentioned Newton's inequality. This post will explore this inequality.

Let x be a list of real numbers and define S_n(x) to be the average over all products of n elements from x. Newton's inequality says that

S_n-1 S_n+1 S^2_n

In more terminology more recent than Newton, we say that the sequence S_n is log-concave.

The name comes from the fact that if the elements of x are positive, and hence the Ss are positive, we can take the logarithm of both sides of the inequality and have

(log S_n-1 + log S_n+1)/2 log S_n

which is the discrete analog of saying log S_k is concave as a function of k.

Let's illustrate this with some Python code.

from itertools import combinations as Cfrom numpy import randomfrom math import combimport matplotlib.pyplot as pltdef S(x, n): p = lambda c: prod([t for t in c]) return sum(p(c) for c in C(x, n))/comb(N, n)random.seed(20231010)N = 10xs = random.random(N)ns = range(1, N+1)ys = [log(S(xs, n)) for n in ns]plt.plot(ns, ys, 'o')plt.xlabel(r"$n$")plt.ylabel(r"$\log S_n$")plt.show()

This produces the following plot.

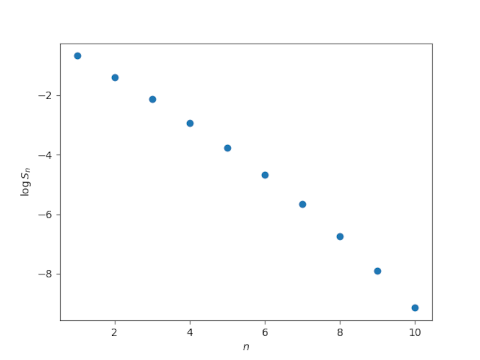
This plot looks nearly linear. It's plausible that it's concave.

The post Newton's inequality and log concave sequences first appeared on John D. Cook.