Means of means bounding the logarithmic mean
The geometric, logarithmic, and arithmetic means of a and b are defined as follows.
A few days ago I mentioned that G L A. The logarithmic mean slips between the geometric and arithmetic means.
Or to put it another way, the logarithmic mean is bounded by the geometric and arithmetic means. You can bound the logarithmic mean more tightly with a mixture of the geometric and arithmetic means.
In [1] the authors show that
Note that the leftmost expression is the geometric mean of G, G, and A, and the rightmost expression is the arithmetic mean of G, G, and A. We can write this as
where G with no argument is the geometric mean of a and b and G with three arguments is the geometric mean of those arguments, and similarly for A.
The following plot shows how well these means of means bound the logarithmic mean. We let a = 1 and let b vary from 1 to 10o.
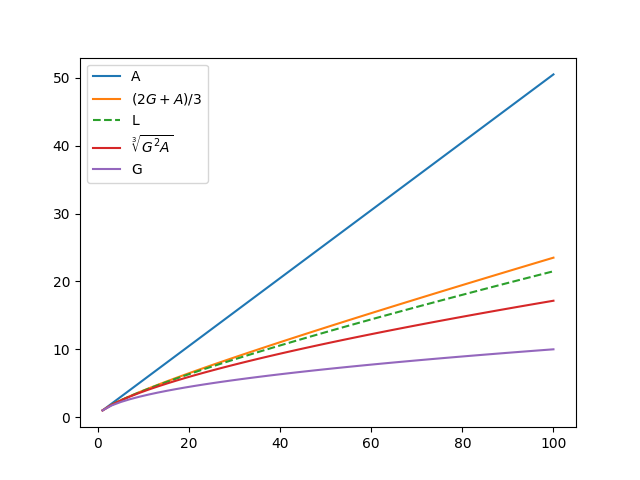
The upper bound is especially tight for moderate values of b. When I first made the plot I let b run up to 10 and there were apparently only four curves in the plot. I had to pick a larger value of b before the curves for L and (2G + A)/3 to be distinguished.
Related posts[1] Graham Jameson and Peter R. Mercer. The Logarithmic Mean Revisited. The American Mathematical Monthly, Vol. 126, No. 7, pp. 641-645
The post Means of means bounding the logarithmic mean first appeared on John D. Cook.