A knight’s tour of an infinite chessboard
Let ^2 be the lattice of points in the plane with integer coordinates. You could think of these points as being the centers of the squares in a chessboard extending to infinity in every direction.
Cantor tells us that the points in ^2 are countable. What's more surprising is that you could count the points using a knight's move. If you place a knight at the origin, there is a way for him to visit every point exactly once.
It's possible to tour every point in a 5 * 5 lattice as shown below.
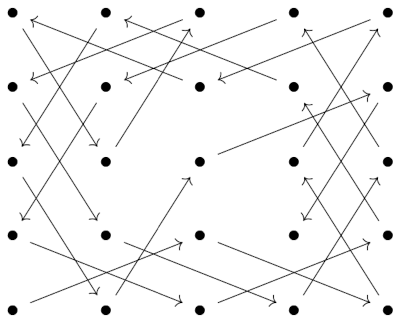
The knight's next move would take it out of the 5 * 5 block and position it to begin touring a new 5 * 5 block bordering the first block.
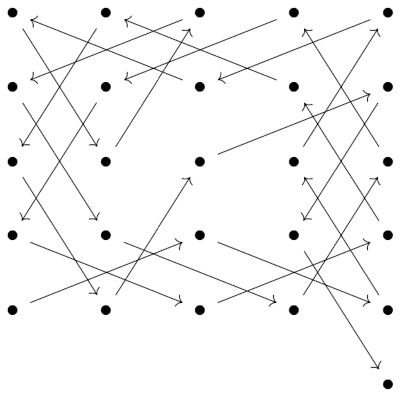
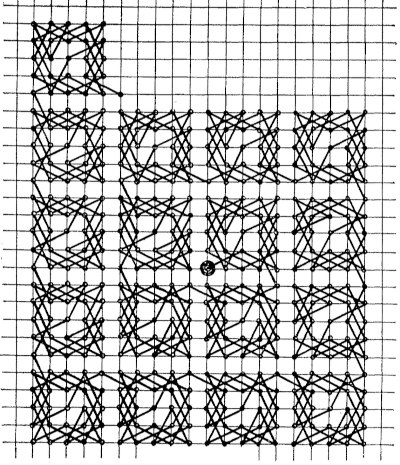
You can repeat this pattern, covering ^2 in a spiral of 5 * 5 squares.
I produced the first two images using Quiver, an application intended for drawing commutative diagrams, though I've found it useful for other drawing tasks as well.
The third image was taken from a note by Robert E. Gilman on an article by Norman Anning: A Recreation. The American Mathematical Monthly, Vol. 37, No. 10 (Dec., 1930), pp. 535-538.
Related postsThe post A knight's tour of an infinite chessboard first appeared on John D. Cook.