A couple more variations on an ancient theme

I've written a couple posts on the approximation

by the Indian astronomer Aryabhata (476-550). The approximation is accurate for x in [-/2, /2].

The first post collected a Twitter thread about the approximation into a post. The second looked at how far the coefficients in Aryabhata's approximation are from the optimal approximation as a ratio of quadratics.

This post will answer a couple questions. First, what value of did Aryabhata have and how would that effect the approximation error? Second, how bad would Aryabhata's approximation be if we used the approximation ^2 10?

Using Aryabhata's value of

Aryabhata knew the value 3.1416 for . We know this because he said that a circle of diameter 20,000 would have circumference 62,832. We don't know, but it's plausible that he knew to more accuracy and rounded it to the implied value.

Substituting 3.1416 for changes the sixth decimal of the approximation, but the approximation is good to only three decimal places, so 3.1416 is as good as a more accurate approximation as far as the error in approximating cosine is concerned.

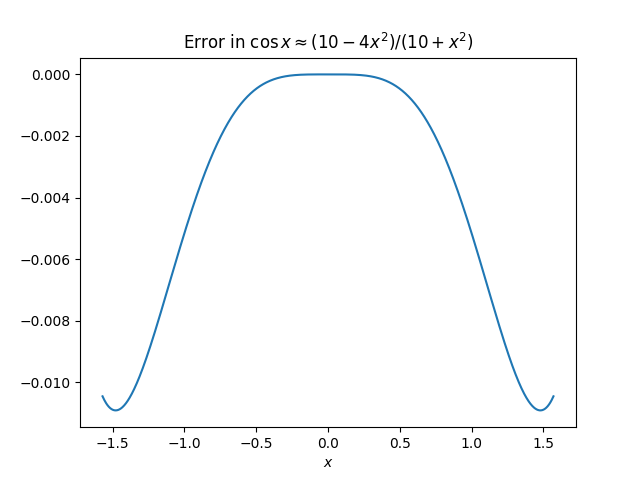
Using ^2 10

Substituting 10 for ^2 in Aryabhata's approximation gives an approximation that's convenient to evaluate by hand.

It's very accurate for small values of x but the maximum error increases from 0.00163 to 0.01091. Here's a plot of the error.

The post A couple more variations on an ancient theme first appeared on John D. Cook.