Binomial bound

I recently came across an upper bound I hadn't seen before [1]. Given a binomial coefficient C(r, k), let

n = min(k, r - k)

and

m = r - n.

Then for any > 0,

C(n + m, n) (1 + )^{n + m} / ⁿ.

The proof follows quickly from applying the binomial theorem to (1 + )^{n + m}.

I could imagine how non-optimal choice of could be convenient in some context, it's natural to want to see how good the upper bound is for the best , which works out to be = n/m.

A little algebra shows this value of leads to

C(n + m, n) (n + m)^{n + m} / nⁿ m^m.

Note that while the original bound is not symmetric inn and m, the optimal bound is.

Returning to the original notation C(r, k), let's see how tight the optimal bound is by plotting, as a function of r, the maximum relative error as a k varies.

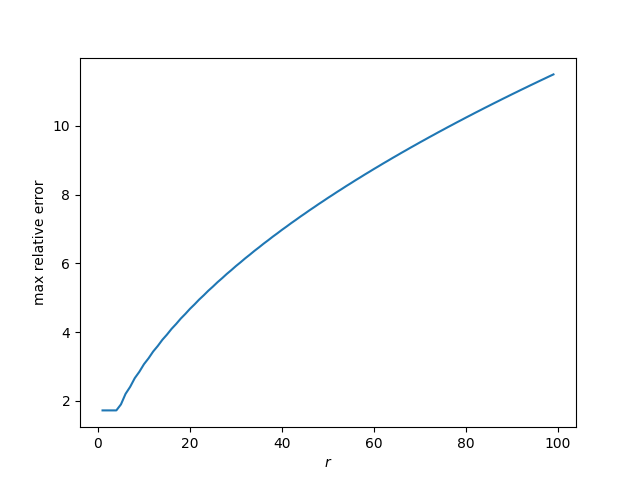
The maximum relative error, over the range plotted, is very roughly r/10.

Related posts

• Bounds on the central binomial coefficient
• Non-integer binomial coefficients
• q-binomial coefficients

[1] Grzegorz ysik. The -binomial inequality. The Mathematical Gazette. Vol. 92, No. 523 (March 2008), pp. 97-99

The post Binomial bound first appeared on John D. Cook.