Band-limited expansion
The band-limited expansion of the function f(x) is given by
where sinc(x) = sin(x)/x. This is also called the sinc expansion, or the Whittaker cardinal after its discoverer E. T. Whittaker [1].
This is called the band-limited expansion of f because each term in the infinite sum is band-limited, i.e. only has Fourier spectrum within a finite band, because the Fourier transform of the sinc function is a step function supported between -1/2 and 1/2. [2]
The band-limited expansion has a lot of nice mathematical properties, leading Whittaker to call it a function of royal blood in the family of entire functions, whose distinguished properties separate it from its bourgeois brethren."
We can find a band-limited approximation for f by taking only a finite number of terms in the sum. An advantage of the band-limited approximation over a truncated Fourier series is that the former converges faster, making it useful in numerical algorithms [3]. Here's an example of approximating the function exp(-x^2) by takingh = 1 and using three terms, i.e. k running from -1 to 1.
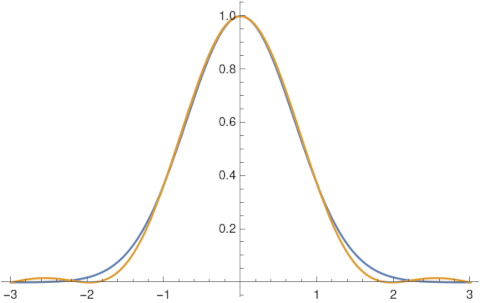
You can improve the accuracy of the approximation by decreasing the size of h or by increasing N. This post explains how to pick the trade-off between h and N to minimize approximation error.
Related posts[1] E. T. Whittaker, On the functions which are represented by the expansions of the interpolation theory, Proc. Roy. Soc. Edinburgh, 35 (1915), pp. 181-194.
[2] You may get a different interval of support if you use a different convention for defining the Fourier transform. Unfortunately there are many conventions.
[3] Frank Stenger. Numerical Methods based on Whittaker Cardinal, or Sinc Functions. Source: SIAM Review, Apr., 1981, Vol. 23, No. 2 (Apr., 1981), pp. 165-224
The post Band-limited expansion first appeared on John D. Cook.