Normal probability approximation
by John from John D. Cook on (#6T1K5)
The previous post presented an approximation
for -1 x 1 and said that it was related to a probability function. This post will make the connect explicit.
LetX be a normally distributed random variable with mean and variance ^2. Then the CDF of X is
So if = 0 and ^2 = 1/2 then we have the following.
Here's Python code to show how good the approximation is.
from numpy import sin, linspace, sqrt, pi from scipy.stats import norm import matplotlib.pyplot as plt x = linspace(-1, 1, 200) X = norm(0, sqrt(0.5)) plt.plot(x, X.cdf(x) - X.cdf(0)) plt.plot(x, sin(sin(x))/sqrt(pi)) plt.legend(["exact", "approx"]) plt.xlabel("$x$") plt.ylabel(r"$P(X \leq x)$")Here's the resulting plot:
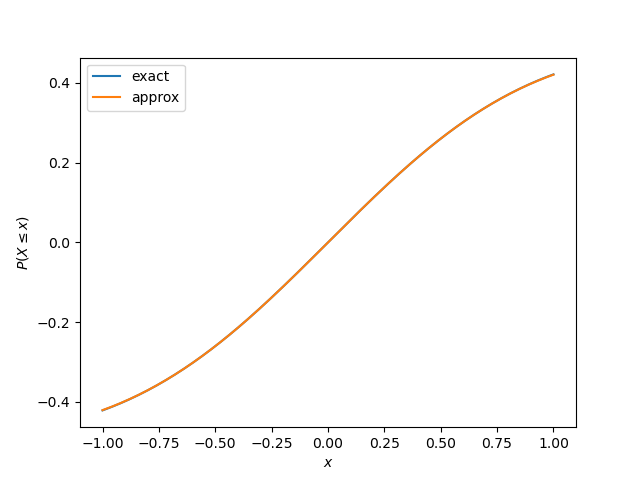
The orange curve for the plot of the approximation completely covers the blue curve of the exact value. The two curves are the same to within the resolution of the plot. See the previous post for a detailed error analysis.
The post Normal probability approximation first appeared on John D. Cook.