Complex golden convergence
The previous post looked at how iterations of
converge to the golden ratio . That post said we could start at any positive x. We could even start at any x > -3/4 because that would be enough for the derivative of (1 + x) to be less than 1, which means the iteration will be a contraction.
We can't start at any x less than -1 because then our square root would be undefined, assuming we're working over real numbers. But what if we move over to the complex plane?
If f is a real-valued function of a real variable and|f'(x)| is bounded by a constant less than 1 on an interval, then f is a contraction on that interval. Is the analogous statement true for a complex-valued function of a complex variable? Indeed it is.
If we start at a distance at least 1/4 away from -1 then we have a contraction and the iteration converges to . If we start closer than that to -1, then the first step of the iteration will throw us further out to where we then converge.
To visualize the convergence, let's look at starting at a circle of points in a circle of radius 10 around and tracing the path of each iteration.
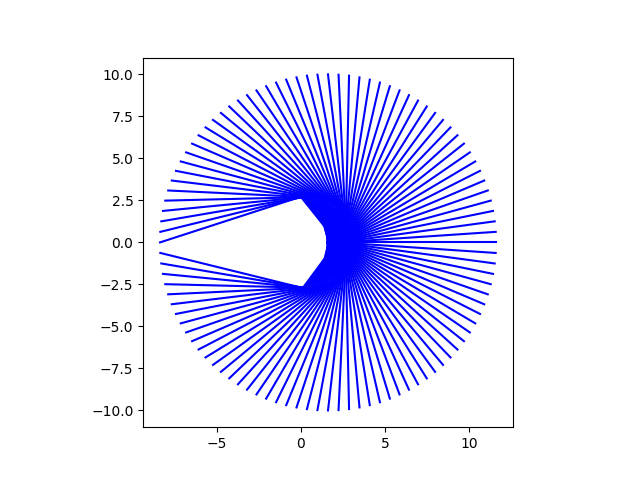
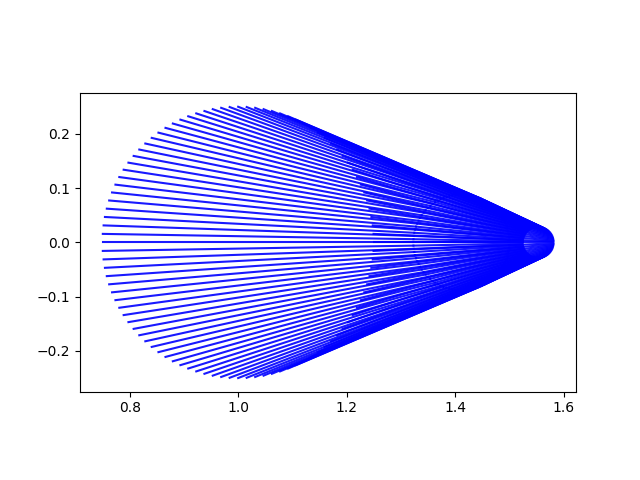
For most of the starting points, the iterations converge almost straight toward , but points near the negative real axis take a more angular path. The gap in the plot is an artifact of iterations avoiding the disk of radius 1/4 around -1. Let's see what happens when we start on the boundary of this disk.
Next, instead of connecting each point to its next iteration, let's plot the starting circle, then the image of that circle, and the image of that circle, etc.

The boundary of the disk, the blue circle, is mapped to the orange half-circle, which is then mapped to the green stretched half circle, etc.
Related postsThe post Complex golden convergence first appeared on John D. Cook.