A Continental Divide for Newton’s Method
Newton's method is a simple and efficient method for finding the roots of equations, provided you start close enough to the root. But determining the set of starting points that converge to a given root, or converge at all, can be very complicated.
In one case it is easy to completely classify where points converge. Suppose you have a quadratic polynomial p(x) with distinct roots a and b in the complex plane. The line perpendicular to the line between a andb is a sort of continental divide, splitting the plane into two watersheds. If you start Newton's method at any point on a root's side of the line, it will converge to that root.
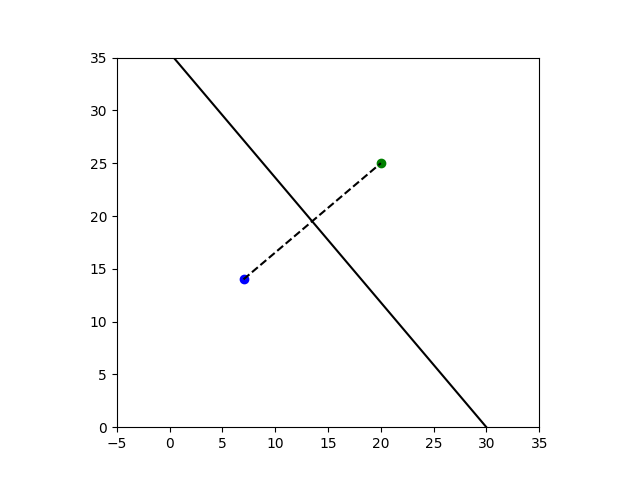
To illustrate this, we will set a = 7 + 14i andb = 20 + 25i,and use Newton's method to find the roots of
p(z) = (z -a)(z -b).
You can start far from the root and still converge, which isn't typical but is the case for quadratic polynomials.
And the point you'll converge to is determined by which side of the continental divide you start on. For example, the following code shows that if you start at 1000 + 2000i you will converge to 20 + 25i.
a = 7 + 14jb = 20 + 25jp = lambda z: (z - a)*(z - b)pprime = lambda z: (z - a) + (z - b)newton = lambda z: z - p(z)/pprime(z)z = 1000 + 2000jfor _ in range(12): z = newton(z) print(z)
If you're not familiar with Python, note that it uses j for the imaginary unit. Here's why.
Things are more complicated if you start Newton's method exactly on the line dividing the two watersheds. The method will not converge. There is a dense set of starting points on the line that will cycle through a finite number of points. And there is a dense set of points that lead to division by zero. (See HAKMEM, item 3.)
Related postsThe post A Continental Divide for Newton's Method first appeared on John D. Cook.