Tiny Jubjub

A few days ago I wrote about the Jubjub elliptic curve that takes its name from Lewis Carroll's poem Jabberwocky. I've also written about a slightly smaller but still enormous curve named Baby Jubjub.

This post introduces Tiny Jubjub, an elliptic curve with 20 elements, one designed to have some properties in common with its gargantuan counterparts, but small enough to work with by hand. As far as I know, the curve was created for the book The Moon Math Manual to zk-SNARKs and may not be known anywhwere outside that book.

First, a word about the book. The math behind zero-knowledge proofs is complicated and unfamiliar to most, and has been called moon math." The zk" in the title stands for zero-knowledge. SNARK stands for succinct non-interactive argument of knowledge." The book is an introduction to some of the mathematics and computer science used in the Zcash privacy coin.

Equation and size

The Tiny Jubjub curve, abbreviated TJJ, has Weierstrass form

y^2 = x^3 + 8x + 8

and is defined over the field F₁₃, the integers mod 13. As mentioned above, it has 20 points. This is interesting because it is close to Hesse's upper bound on the number of points on an elliptic curve as a function of the field size. In all the examples in my post from a couple days ago the number of points on each curve was equal to slightly below the middle of the possible range.

Here's a checkerboard plot of TJJ, like the plots given here.

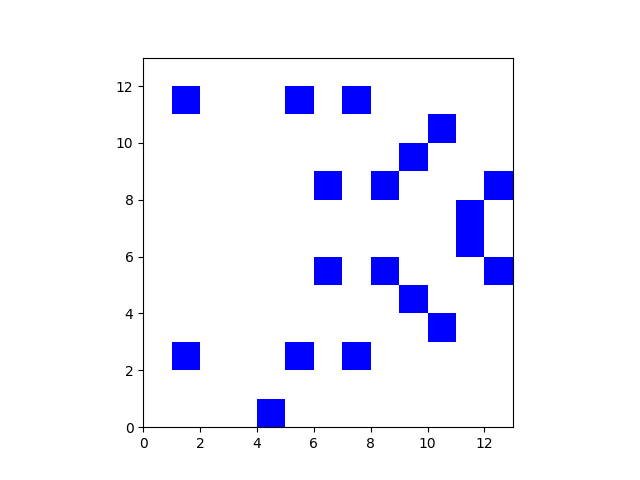
Note that there are 19 blue squares above. Elliptic curves always have an extrapoint at infinity not shown.

Montgomery form

One thing Tiny Jubjub has in common with the better known Jubjub curves is that it has a Montgomery form. That is, there is a change of variables that puts the curve in the form

By^2 = x^3 + Ax + b

with B(A^2 - 4) 0. Every elliptic curve in Montgomery form can be put in Weierstrass form, but not vice versa; Montgomery curves are special.

TJJ can be put in Montgomery form withA = 6 and B = 7.

Twisted Edwards form

Every elliptic curve that can be put into Montgomery form can also be put into twisted Edwards form

a x^2 + y^2 = 1 + d x^2 y^2

witha 0 d.

TJJ can be put into Montgomery form witha = 3 and d = 8.

It's useful when a curve can be put in twisted Edwards form because elliptic curve arithmetic can be implemented without branching logic for special cases.

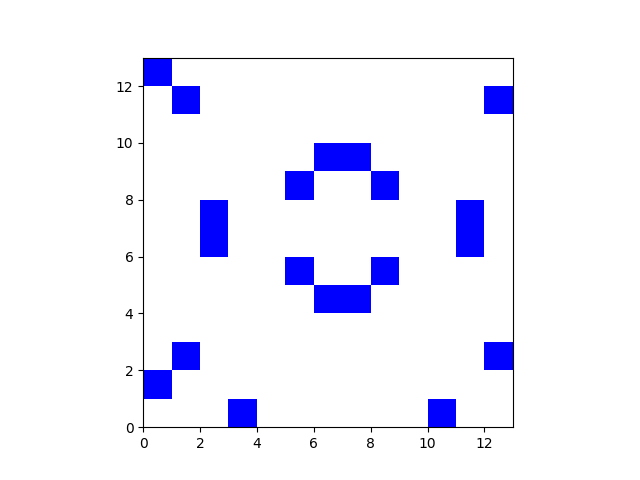
Note that this plot has 20 blue squares. That's because for Montgomery curves, the point at infinity is (0, 1), and so it falls inside the grid we're plotting.

SNARK friendly

TJJ is a SNARK-friendly curve, which is why it appears often in a book on zk-SNARKs. A curve is said to be SNARK friendly if in its twisted Edwards forma is a quadratic residue andd is not. In our case, that means

x^2 = 3 mod 13

has a solution but

x^2 = 8 mod 13

does not. We can verify this with the following Python code.

 >>> [x**2 % 13 for x in range(13)] [0, 1, 4, 9, 3, 12, 10, 10, 12, 3, 9, 4, 1]

Notice that 3 is in the output and 8 is not.

Related posts

• Pallas, Vesta, and Zcash
• Legendre and Ethereum
• Monero's elliptic curve

The post Tiny Jubjub first appeared on John D. Cook.