Randomly generated dragon

Here's a simple way to generate a fractal known as the Twin Dragon. Start with random values of x andy and repeatedly update the according to the rule

x_new = (- x_old + y_old)/2 - b
y_new = (- x_old - y_old)/2

where b is randomly chosen to be 0 or 1 with equal probability. The plot of these points fills in the Twin Dragon.

Here's what the plot looks like after 10,000 iterations.

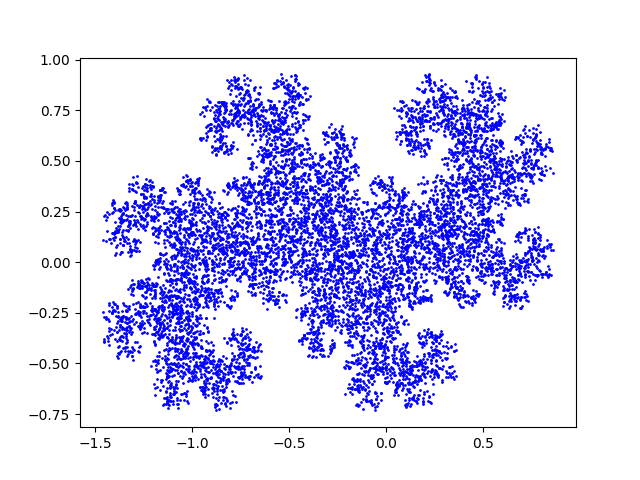
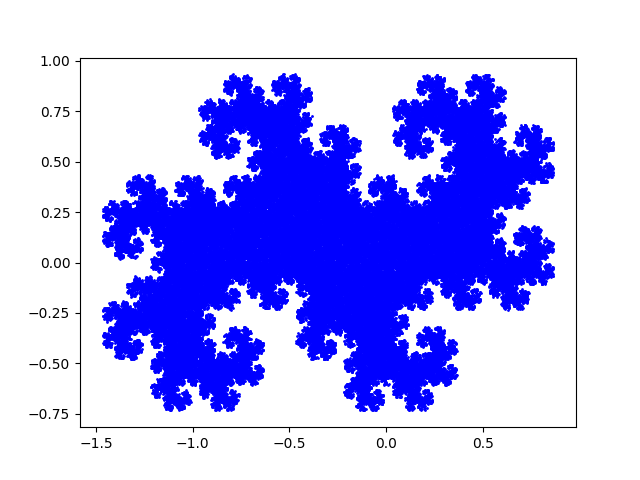
And after 100,000 iterations.

Here's the Python script I used to make the plots.

import matplotlib.pyplot as pltfrom numpy.random import random, choicex, y = random(), random()for _ in range(100000): x, y = (-x + y)/2, (-x - y)/2 x -= choice([0, 1]) plt.plot(x, y, 'bo', markersize=1)plt.show()

The algorithm used here is a particularly special case of a more general algorithm for generating similar fractals found in [1].

Here's a similar post from several years ago:
The chaos game and the Sierpinski triangle

[1] Darst, Palagallo, and Price. Fractal Tilings in the Plane. Mathematics Magazine [71]:1, 1998.

The post Randomly generated dragon first appeared on John D. Cook.