Minimalist Mandelbrot set

The Mandelbrot set is one of the most famous fractals. It consists of the complex numbers c such that iterations of

f(z) = z^2 + c

are bounded. The plot of the Mandelbrot set is a complicated image-it's a fractal, after all-and yet there's a simple description of an first approximation to the Mandelbrot set.

As shown in [1], the image of the disk

A = { : || < }

under the map taking z to z - z^2 gives the set of all points where iterations off converge to a point.

Also show in [1] is that the points

B = {c : |1 +c| < 1/4}

are the ones such thatf(f(z)) converges to a fixed point.

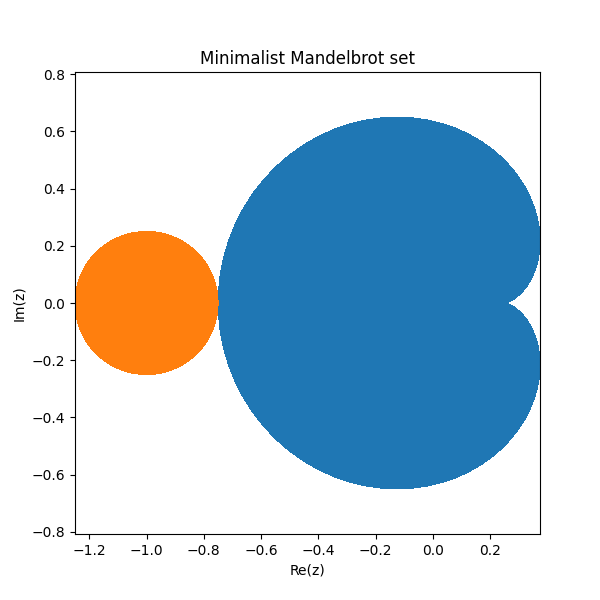
These two parts form the core of the Mandelbrot set. The blue heart-shaped region on the right is A and the orange disk on the left is B.

The rest of the Mandelbrot set are the points where iterations off remain bounded but have more complicated behavior than the points inA or B.

[1] Alan F. Beardon. Iteration of Rational Functions. Springer-Verlag, 1991.

The post Minimalist Mandelbrot set first appeared on John D. Cook.