Randomly selecting points inside a triangle
If you have a triangle with verticesA,B, andC, how would you generate random points inside the triangleABC?
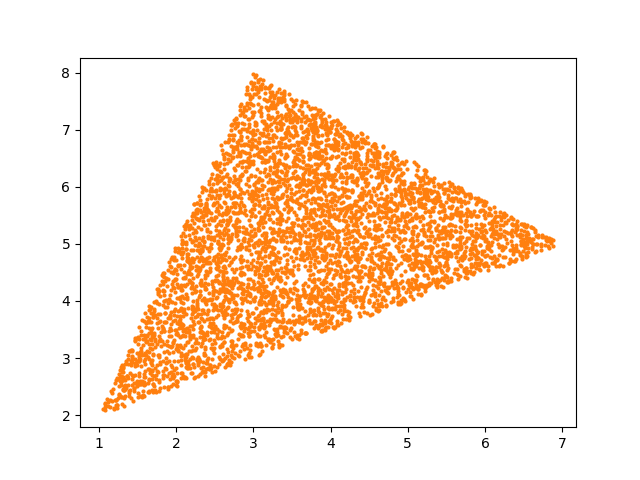
Barycentric coordinatesOne idea would be to use barycentric coordinates.
- Generate random numbers , , and from the interval [0, 1].
- Normalize the points to have sum 1 by dividing each by their sum.
- Return A + B + C.
This generates points inside the triangle, but not uniformly.
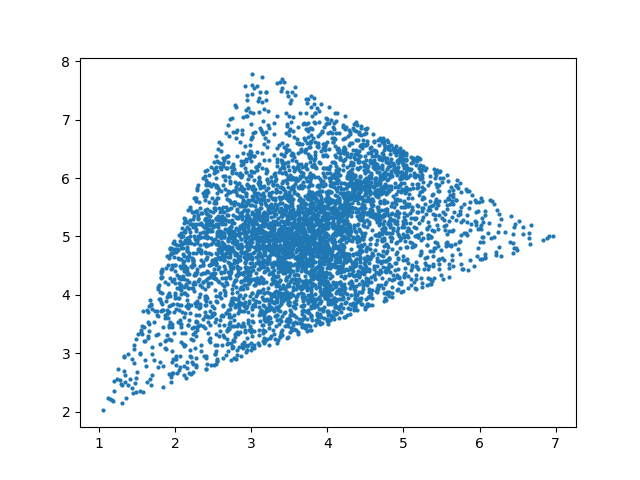
Another idea is to use an accept-reject method. Draw a rectangle around the triangle, generate points in the square, and throw them away if they land outside the triangle.
An advantage to this method is that it obviously works because it doesn't rely on anything subtle. Three cheers for brute force!
The method is fairly efficient; on average only half the points will be rejected.
A disadvantage to all accept-reject methods is that they have variable runtime, though this only matters in some applications.
Accept-flipThere is a clever variation on the accept-reject method. Create a parallelogram by attaching a flipped copy of the triangle. Now randomly sample from the parallelogram. Every sample point will either land inside the original triangle or in its flipped twin. If it landed in the original triangle, keep it. If it landed in the twin, flip it back over and use that point.
This is like an accept-reject method, except there's no waste. Every point is kept, possibly after flipping.
You can find code for implementing this method on Stack Overflow.
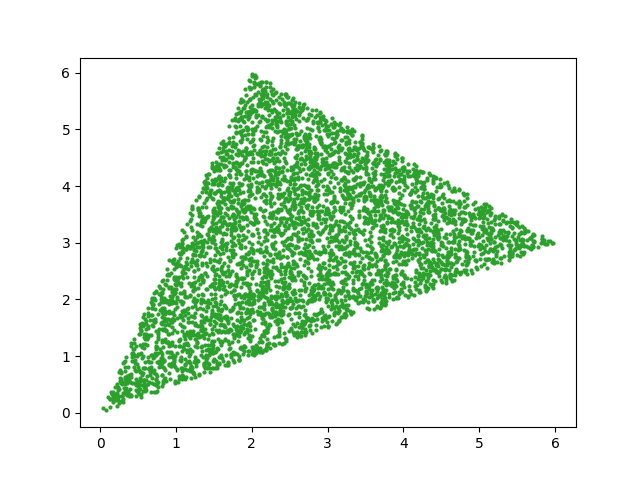
Felix left a note in the comments that the barycentric approach would work if you draw the random weights from an exponential distribution rather than a uniform distribution. That goes against my intuition. I thought about using a different distribution on the weights, but I didn't work out what it would need to be, but I did not expect it to be exponential. Apparently it works. Here's a proof by plot: