A triangle inequality by Erdős

Plane geometry has been studied since ancient times, and yet new results keep being discovered millennia later, including elegant results. It's easy to come up with a new result by proving a complicated theorem that Euclid would not have cared about. It's more impressive to come up with a new theorem that Euclid would have understood and found interesting.

Paul Erds conjectured another triangle inequality in 1935 which was proved by Mordell and Barrow in 1937 [1].

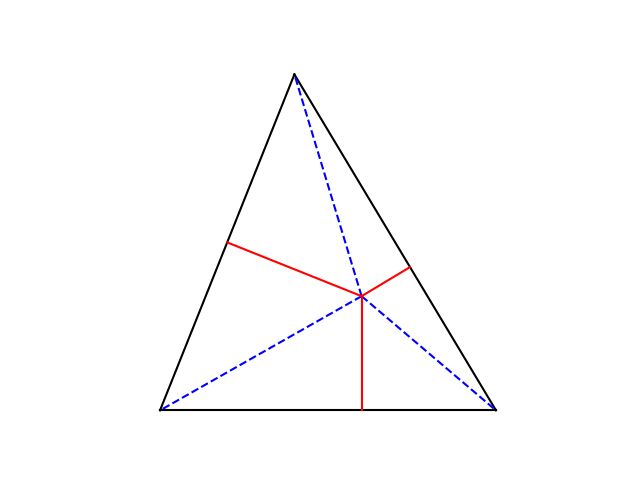
Let P be a point inside a triangle ABC. Let x, y, z be the distances fromP to the vertices and let p, q, r, be the distances to the sides. Then

x +y +z >= 2(p +q +r)

with equality only ifP is the center of an equilateral triangle [2]. In the figure above, the theorem says the dashed blue lines together are more than twice as long as the solid red lines.

How far apart are the left and right sides of the inequality? This was the motivation for the previous post on selecting random points from a triangle. I wanted to generate random points and compare the two sides of the Erds-Mordell-Barrow inequality.

We can visualize the inequality by generating random points inside the triangle and plotting the points with a color that indicates the inequality gap, darker blue corresponding to a larger gap.

This shows the inequality is sharper in the middle of the triangle than near the vertices.

[1] Problem 3740, American Mathematical Monthly, 44 (1937) 252-254.

[2] You could interpret this as a theorem comparing barycentric and trilinear coordinates.

The post A triangle inequality by Erds first appeared on John D. Cook.