log2(3) and log2(5)

AlmostSure on X pointed out that

log₂ 3 19/12,

an approximation that's pretty good relative to the size of the denominator. To get an approximation that's as accurate or better requires a larger denominator for log₂ 5.

log₂ 5 65/28

This above observations are correct, but are they indicative of a more general pattern? Is log₂ 3 easier to approximate than log₂ 5 using rational numbers? There are theoretical ways to quantify this-irrationality measures-but they're hard to compute.

If you look at the series of approximations for both numbers, based on continued fraction convergents, thenth convergent for log₂ 5 is more accurate than thenth convergent for log₂ 3, at least for the first 16 terms. After that I ran out of floating point precision and wasn't sufficiently interested to resort to extended precision.

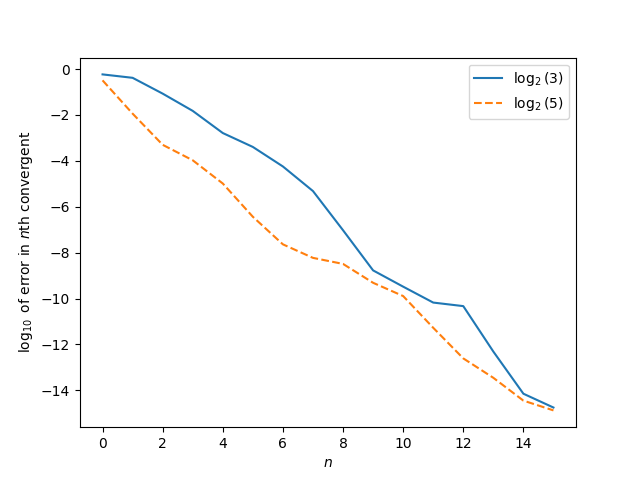
Admittedly this is a non-standard way to evaluate approximation error. Typically you look at the approximation error relative to the size of the denominator, not relative to the index of the convergents.

Here's a more conventional comparison, plotting the log of approximation error against the log of the denominators.

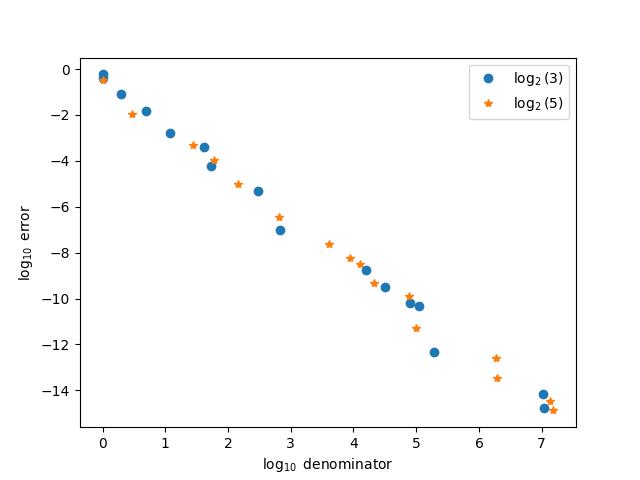
Continued fraction posts

• Continued fractions as matrix products
• Applications of continued fractions
• Calendars and continued fractions

The post log2(3) and log2(5) first appeared on John D. Cook.