Mills ratio and tail thickness
The Mills ratio [1] is the ratio of the CCDF to the PDF. That is, for a random variable X, the Mills ratio at x is the complementary cumulative distribution function divided by the density function. If the density function of X is f, then
The Mills ratio highlights an important difference between the Student t distribution and the normal distribution.
Introductory statistics classes will say things like you can approximate a t distribution with a normal if it has more than 30 degrees of freedom." That may be true, depending on the application. At(30) distribution and a normal distribution behave similarly in the middle but not in the tails.
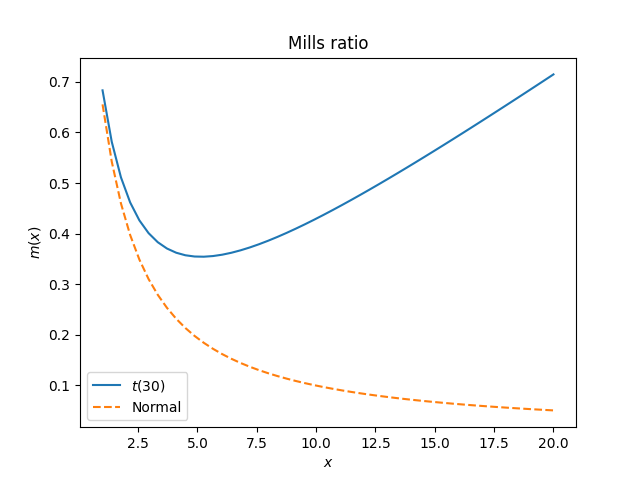
The Mills ratio for at distribution with degrees of freedom is asymptotically x/, while the Mills ratio for a standard normal distribution is asymptotically 1/x. Note that increasing does make the Mills function smaller, but it still eventually grows linearly whereas the Mills function of a normal distribution decays linearly.
In general, the Mills ratio is a decreasing function for thin-tailed distributions and an increasing function for fat-tailed distributions. The exponential distribution is in the middle, with constant Mills function.
Related posts[1] Named after John P. Mills, so there's no apostrophe before thes.
The post Mills ratio and tail thickness first appeared on John D. Cook.