Large scale microwave trapped ion universal quantum computer design can scale to billions trapped ions and would solve 2048 bit Shor factoring in 110 days
by noreply@blogger.com (brian wang) from NextBigFuture.com on (#2B8QZ)
The microwave trapped ion universal quantum computer design work features a new invention permitting actual quantum bits to be transmitted between. individual quantum computing modules in order to obtain a fully modular large-scale machine capable of reaching nearly arbitrary large computational processing powers.
Previously, scientists had proposed using fibre optic connections to connect individual computer modules. The new invention introduces connections created by electric fields that allow charged atoms (ions) to be transported from one module to another. This new approach allows 100,000 times faster connection speeds between individual quantum computing modules compared to current state-of-the-art fibre link technology.
The new blueprint is the work of an international team of scientists from the University of Sussex (UK), Google (USA), Aarhus University (Denmark), RIKEN (Japan) and Siegen University (Germany).
They estimate that a 2 billion trapped ion system could be used to crack 2048 bit encryption in 110 days. In December 2009, Lenstra and his team announced the factorization of a 768-bit RSA modulus.
In 2012, a 923 bit code was cracked using 21 computers
The Lenstra group estimated that factoring a 1024-bit RSA modulus would be about 1,000 times harder than their record effort with the 768-bit modulus, or in other words, on the same hardware, with the same conditions, it would take about 1,000 times as long. They also estimated that their record achievement would have taken 1,500 years if they normalized processing power to that of the standard desktop machine at the time - this assumption is based on a 2.2 Ghz AMD Opteron processor with 2GB RAM. Breaking a DigiCert 2048-bit SSL certificate would take about 4.3 billion times longer (using the same standard desktop processing) than doing it for a 1024-bit key. It is therefore estimated, that standard desktop computing power would take 4,294,967,296 x 1.5 million years to break a DigiCert 2048-bit SSL certificate. Or, in other words, a little over 6.4 quadrillion years.
As a next step, the team will construct a prototype quantum computer, based on this design, at the University.
The effort is part of the UK Government's plan to develop quantum technologies towards industrial exploitation and makes use of a recent invention by the Sussex team to replace billions of laser beams required for quantum computing operations within a large-scale quantum computer with the simple application of voltages to a microchip.
Professor Hensinger said: "The availability of a universal quantum computer may have a fundamental impact on society as a whole. Without doubt it is still challenging to build a large-scale machine, but now is the time to translate academic excellence into actual application building on the UK's strengths in this ground-breaking technology. I am very excited to work with industry and government to make this happen."
The computer's possibilities for solving, explaining or developing could be endless. However, its size will be anything but small. The machine is expected to fill a large building, consisting of sophisticated vacuum apparatus featuring integrated quantum computing silicon microchips that hold individual charged atoms (ions) using electric fields.
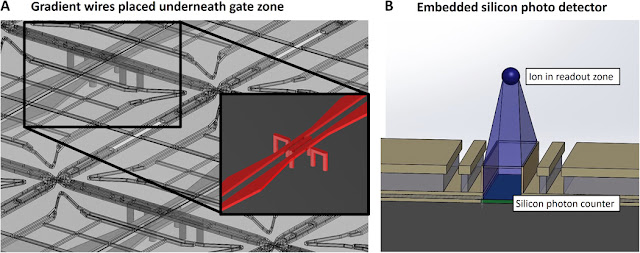
In previously proposed trapped ion quantum computing architectures, modules are powered by laser-driven single- and multiqubit gates. However, the vast amount of individually controlled and stabilized laser beams required in such architectures would make the required engineering to build a large-scale quantum computer challenging. Here, we propose an architecture that is based on a concept involving global long-wavelength radiation and locally applied magnetic fields. The gate interactions are based on a mechanism first proposed by Mintert and Wunderlich in 2001, making use of magnetic field gradients within dedicated gate zones. Only global laser light fields are required for loading, Doppler cooling, and state preparation and readout of ions, whereas laser-driven quantum gates requiring careful alignment in each gate zone are not required in our approach. Large-scale quantum computers, which rely on laser gates and are capable of solving classically intractable problems, may require millions of individual laser beams that have to be precisely aligned with respect to individual entanglement regions and need to be individually controlled. In our microwave-based architecture, all laser fields do not have to be precisely aligned or individually controlled. However, one should note that our architecture still incorporates a number of technical challenges, such as the creation of strong magnetic field gradients and the requirement of calibration operations and well-controlled voltages, which are required to execute quantum gates. We present the blueprint for a scalable microwave trapped ion quantum computer module, which is based on today's silicon semiconductor and ion trap technology. The modules, driven by global laser and microwave fields, perform ion loading and ion shuttling, generate locally addressable magnetic fields as well as magnetic field gradients to perform single- and multiqubit gates, and feature on-chip photo detectors for state readout. All gate, shuttling, and state readout operations are controlled by on-chip electronics, and a cooling system is integrated into the module to allow for efficient temperature management. Each module, when placed in an ultrahigh vacuum (UHV) system and powered by global laser and microwave fields, operates as a modular stand-alone quantum computer.

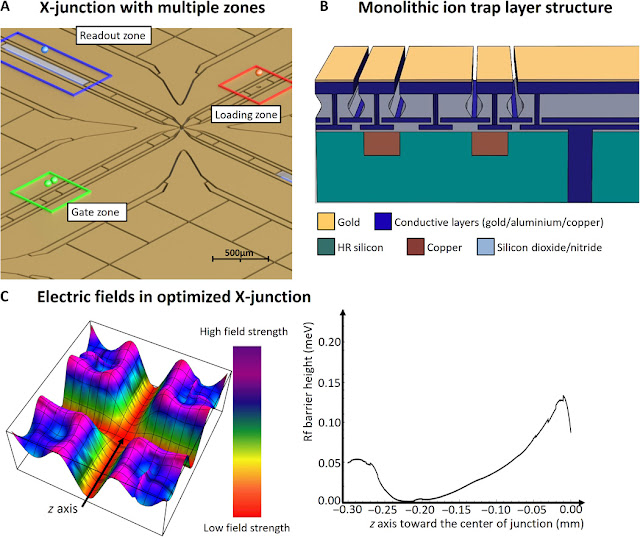
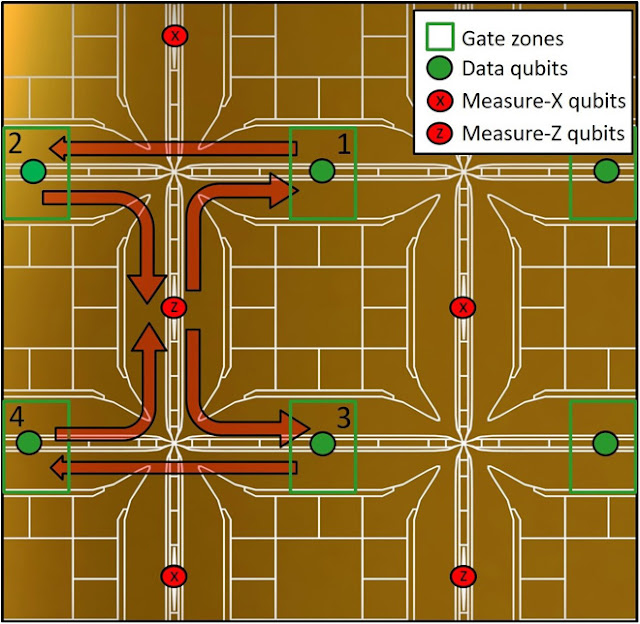
They propose a blueprint for a scalable quantum computer module, which makes use of the discussed microwave-based multiqubit gate scheme and is fabricated using silicon microfabrication technology. Each module is a unit cell for a large-scale quantum computer and features microfabricated ion trap X-junction arrays. In each X-junction, two or more ions are trapped and feature up to three different zones including a microwave-based gate zone, a state readout zone, and a loading zone. Once an ion is trapped in the loading zone, high-fidelity ion shuttling operations transfer the ion to the gate zone. There, ions can be individually addressed using locally adjustable magnetic fields and entangled using static magnetic field gradients in conjunction with global microwave and rf fields. When the state of the qubit needs to be detected, the ion is transferred to the readout zone, where global laser fields and on-chip photo detectors are used for state readout. A second ion species is used to sympathetically cool the qubit ion without affecting its internal states. All coherent quantum operations are performed and controlled by on-chip electronics, relying only on global microwave and rf fields. In our microwave-based architecture, laser light is only required for state preparation and detection, photoionization, and sympathetic cooling. The required laser beams have much less stringent requirements than laser beams for quantum gate realization. The laser beams do not need to have high intensity, and do not need to be phase-stable; the mode profile only requires some overlap with the ion to scatter sufficient photons. Laser beams for sympathetic cooling can even be provided as sheets.
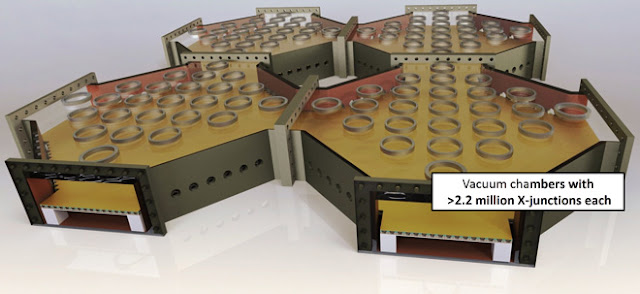
On the basis of the same scheme, they can give quantitative estimates on the system size and processing time for a machine that solves a relevant, hard problem, such as the Shor factoring of a 2048-bit number. For the calculations, they assume a single-qubit gate time of 2.5 I1/4s, two-qubit gate time of 10 I1/4s, ion separation and shuttling time of 15 I1/4s each, static magnetic field gradient ramp-up and ramp-down time of 5 I1/4s each, and a measurement time of 25 I1/4s, resulting in a total error correction cycle time of 235 I1/4s. On the basis of these numbers, performing a 2048-bit number Shor factorization will take on the order of 110 days and require a system size of 2 billion trapped ions. Shor factoring of a 1024-bit number will take on the order of 14 days. Both of these factorizations will require almost the same amount of physical qubits because the required pace of the ancilla qubit generation is the same for a 2048-bit and a 1024-bit factorization. Trapping 2 billion ions will require 23 i- 23 vacuum chambers occupying an area of ca. 103.5 i- 103.5 m2.
Science Advances - Blueprint for a microwave trapped ion quantum computer
Read more










Previously, scientists had proposed using fibre optic connections to connect individual computer modules. The new invention introduces connections created by electric fields that allow charged atoms (ions) to be transported from one module to another. This new approach allows 100,000 times faster connection speeds between individual quantum computing modules compared to current state-of-the-art fibre link technology.
The new blueprint is the work of an international team of scientists from the University of Sussex (UK), Google (USA), Aarhus University (Denmark), RIKEN (Japan) and Siegen University (Germany).
They estimate that a 2 billion trapped ion system could be used to crack 2048 bit encryption in 110 days. In December 2009, Lenstra and his team announced the factorization of a 768-bit RSA modulus.
In 2012, a 923 bit code was cracked using 21 computers
The Lenstra group estimated that factoring a 1024-bit RSA modulus would be about 1,000 times harder than their record effort with the 768-bit modulus, or in other words, on the same hardware, with the same conditions, it would take about 1,000 times as long. They also estimated that their record achievement would have taken 1,500 years if they normalized processing power to that of the standard desktop machine at the time - this assumption is based on a 2.2 Ghz AMD Opteron processor with 2GB RAM. Breaking a DigiCert 2048-bit SSL certificate would take about 4.3 billion times longer (using the same standard desktop processing) than doing it for a 1024-bit key. It is therefore estimated, that standard desktop computing power would take 4,294,967,296 x 1.5 million years to break a DigiCert 2048-bit SSL certificate. Or, in other words, a little over 6.4 quadrillion years.
As a next step, the team will construct a prototype quantum computer, based on this design, at the University.




The effort is part of the UK Government's plan to develop quantum technologies towards industrial exploitation and makes use of a recent invention by the Sussex team to replace billions of laser beams required for quantum computing operations within a large-scale quantum computer with the simple application of voltages to a microchip.
Professor Hensinger said: "The availability of a universal quantum computer may have a fundamental impact on society as a whole. Without doubt it is still challenging to build a large-scale machine, but now is the time to translate academic excellence into actual application building on the UK's strengths in this ground-breaking technology. I am very excited to work with industry and government to make this happen."
The computer's possibilities for solving, explaining or developing could be endless. However, its size will be anything but small. The machine is expected to fill a large building, consisting of sophisticated vacuum apparatus featuring integrated quantum computing silicon microchips that hold individual charged atoms (ions) using electric fields.
In previously proposed trapped ion quantum computing architectures, modules are powered by laser-driven single- and multiqubit gates. However, the vast amount of individually controlled and stabilized laser beams required in such architectures would make the required engineering to build a large-scale quantum computer challenging. Here, we propose an architecture that is based on a concept involving global long-wavelength radiation and locally applied magnetic fields. The gate interactions are based on a mechanism first proposed by Mintert and Wunderlich in 2001, making use of magnetic field gradients within dedicated gate zones. Only global laser light fields are required for loading, Doppler cooling, and state preparation and readout of ions, whereas laser-driven quantum gates requiring careful alignment in each gate zone are not required in our approach. Large-scale quantum computers, which rely on laser gates and are capable of solving classically intractable problems, may require millions of individual laser beams that have to be precisely aligned with respect to individual entanglement regions and need to be individually controlled. In our microwave-based architecture, all laser fields do not have to be precisely aligned or individually controlled. However, one should note that our architecture still incorporates a number of technical challenges, such as the creation of strong magnetic field gradients and the requirement of calibration operations and well-controlled voltages, which are required to execute quantum gates. We present the blueprint for a scalable microwave trapped ion quantum computer module, which is based on today's silicon semiconductor and ion trap technology. The modules, driven by global laser and microwave fields, perform ion loading and ion shuttling, generate locally addressable magnetic fields as well as magnetic field gradients to perform single- and multiqubit gates, and feature on-chip photo detectors for state readout. All gate, shuttling, and state readout operations are controlled by on-chip electronics, and a cooling system is integrated into the module to allow for efficient temperature management. Each module, when placed in an ultrahigh vacuum (UHV) system and powered by global laser and microwave fields, operates as a modular stand-alone quantum computer.

They propose a blueprint for a scalable quantum computer module, which makes use of the discussed microwave-based multiqubit gate scheme and is fabricated using silicon microfabrication technology. Each module is a unit cell for a large-scale quantum computer and features microfabricated ion trap X-junction arrays. In each X-junction, two or more ions are trapped and feature up to three different zones including a microwave-based gate zone, a state readout zone, and a loading zone. Once an ion is trapped in the loading zone, high-fidelity ion shuttling operations transfer the ion to the gate zone. There, ions can be individually addressed using locally adjustable magnetic fields and entangled using static magnetic field gradients in conjunction with global microwave and rf fields. When the state of the qubit needs to be detected, the ion is transferred to the readout zone, where global laser fields and on-chip photo detectors are used for state readout. A second ion species is used to sympathetically cool the qubit ion without affecting its internal states. All coherent quantum operations are performed and controlled by on-chip electronics, relying only on global microwave and rf fields. In our microwave-based architecture, laser light is only required for state preparation and detection, photoionization, and sympathetic cooling. The required laser beams have much less stringent requirements than laser beams for quantum gate realization. The laser beams do not need to have high intensity, and do not need to be phase-stable; the mode profile only requires some overlap with the ion to scatter sufficient photons. Laser beams for sympathetic cooling can even be provided as sheets.
On the basis of the same scheme, they can give quantitative estimates on the system size and processing time for a machine that solves a relevant, hard problem, such as the Shor factoring of a 2048-bit number. For the calculations, they assume a single-qubit gate time of 2.5 I1/4s, two-qubit gate time of 10 I1/4s, ion separation and shuttling time of 15 I1/4s each, static magnetic field gradient ramp-up and ramp-down time of 5 I1/4s each, and a measurement time of 25 I1/4s, resulting in a total error correction cycle time of 235 I1/4s. On the basis of these numbers, performing a 2048-bit number Shor factorization will take on the order of 110 days and require a system size of 2 billion trapped ions. Shor factoring of a 1024-bit number will take on the order of 14 days. Both of these factorizations will require almost the same amount of physical qubits because the required pace of the ancilla qubit generation is the same for a 2048-bit and a 1024-bit factorization. Trapping 2 billion ions will require 23 i- 23 vacuum chambers occupying an area of ca. 103.5 i- 103.5 m2.
Science Advances - Blueprint for a microwave trapped ion quantum computer
Read more