Typesetting and computing continued fractions

Pi

The other day I ran across the following continued fraction for I.

Source: L. J. Lange, An Elegant Continued Fraction for I, The American Mathematical Monthly, Vol. 106, No. 5 (May, 1999), pp. 456-458.

While the continued fraction itself is interesting, I thought I'd use this an example of how to typeset and compute continued fractions.

Typesetting

I imagine there are LaTeX packages that make typesetting continued fractions easier, but the following brute force code worked fine for me:

 \pi = 3 + \cfrac{1^2}{6+\cfrac{3^2}{6+\cfrac{5^3}{6+\cfrac{7^2}{6+\cdots}}}}

This relies on the amsmath package for the \cfrac command.

Computing

Continued fractions of the form

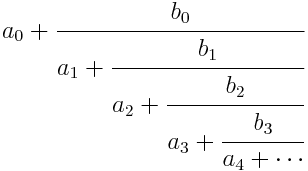
can be computed via the following recurrence. Define A_-1 = 1, A₀ = a₀, B_-1 = 0, and B₀ = 1. Then for k a 1 define A_k+1 and B_k+1 by

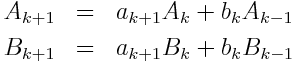
Then the nth convergent the continued fraction is C_n = A_n / B_n.

The following Python code creates the a and b coefficients for the continued fraction for I above then uses a loop that could be used to evaluate any continued fraction.

 N = 20 a = [3] + ([6]*N) b = [(2*k+1)**2 for k in range(0,N)] A = [0]*(N+1) B = [0]*(N+1) A[-1] = 1 A[ 0] = a[0] B[-1] = 0 B[ 0] = 1 for n in range(1, N+1): A[n] = a[n]*A[n-1] + b[n-1]*A[n-2] B[n] = a[n]*B[n-1] + b[n-1]*B[n-2] print( n, A[n], B[n], A[n]/B[n] )

Python uses -1 as a shortcut to the last index of a list. I tack A_-1 and B_-1 on to the end of the A and B arrays to make the Python code match the math notation. This is either clever or a dirty hack, depending on your perspective.

Back to pi

You may notice that these approximations for I are not particularly good. It's a trade-off for having a simple pattern to the coefficients. The continued fraction for I that has all b's equal to 1 has a complicated set of a's with no discernible pattern: 3, 7, 15, 1, 292, 1, 1, etc. However, that continued fraction produces very good approximations. If you replace the first three lines of the code above with that below, you'll see that four iterations produces an approximation to I good to 10 decimal places.

 N = 4 a = [3, 7, 15, 1, 292] b = [1]*N