Typesetting and computing continued fractions
The other day I ran across the following continued fraction for I.

Source: L. J. Lange, An Elegant Continued Fraction for I, The American Mathematical Monthly, Vol. 106, No. 5 (May, 1999), pp. 456-458.
While the continued fraction itself is interesting, I thought I'd use this an example of how to typeset and compute continued fractions.
TypesettingI imagine there are LaTeX packages that make typesetting continued fractions easier, but the following brute force code worked fine for me:
\pi = 3 + \cfrac{1^2}{6+\cfrac{3^2}{6+\cfrac{5^3}{6+\cfrac{7^2}{6+\cdots}}}}This relies on the amsmath package for the \cfrac command.
ComputingContinued fractions of the form
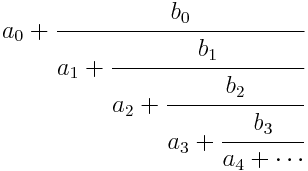
can be computed via the following recurrence. Define A-1 = 1, A0 = a0, B-1 = 0, and B0 = 1. Then for k a 1 define Ak+1 and Bk+1 by
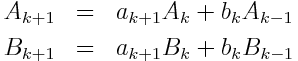
Then the nth convergent the continued fraction is Cn = An / Bn.
The following Python code creates the a and b coefficients for the continued fraction for I above then uses a loop that could be used to evaluate any continued fraction.
N = 20 a = [3] + ([6]*N) b = [(2*k+1)**2 for k in range(0,N)] A = [0]*(N+1) B = [0]*(N+1) A[-1] = 1 A[ 0] = a[0] B[-1] = 0 B[ 0] = 1 for n in range(1, N+1): A[n] = a[n]*A[n-1] + b[n-1]*A[n-2] B[n] = a[n]*B[n-1] + b[n-1]*B[n-2] print( n, A[n], B[n], A[n]/B[n] )
Python uses -1 as a shortcut to the last index of a list. I tack A-1 and B-1 on to the end of the A and B arrays to make the Python code match the math notation. This is either clever or a dirty hack, depending on your perspective.
Back to piYou may notice that these approximations for I are not particularly good. It's a trade-off for having a simple pattern to the coefficients. The continued fraction for I that has all b's equal to 1 has a complicated set of a's with no discernible pattern: 3, 7, 15, 1, 292, 1, 1, etc. However, that continued fraction produces very good approximations. If you replace the first three lines of the code above with that below, you'll see that four iterations produces an approximation to I good to 10 decimal places.
N = 4 a = [3, 7, 15, 1, 292] b = [1]*N