Seattle-Vancouver High Speed Rail Part 2: Everett to Bellingham

San Juan Islands from Chuckanut Drive south of Bellingham (Photo by the author)

In Part 1 of this series we looked at the Seattle-Everett segment of a potential high speed rail (HSR) service between Seattle and Vancouver B.C. We looked at the paucity of available right-of-way, the likelihood of repurposing the I-5 express lanes, and the topographical challenges involved in descending from 500"^2 in South Everett to a sea-level Everett Station. In Part 3 we'll look at the approach into Vancouver, and in Part 4 we'll look at inland routes and ideas for suburban terminals. But for today's Part 2 let's look at the middle third of the trip, from Everett to Bellingham.

For HSR trips between major cities, the highest speeds are usually reached in the intermediate rural areas, with slower approach speeds to the anchor cities being relatively common. So we would reasonably expect to fly through the farmlands of Snohomish and Skagit Counties. How would we do it?

However we've gotten our train to Everett Station, when looking north from Everett we are immediately confronted with a different set of challenges. First and foremost, the first several miles into Marysville would be through the wetland sloughs of the Snohomish River's outlet into Puget Sound. The current trip from Everett to Marysville creaks across slow drawbridges before picking up speed in North Marysville. Environmental challenges aside, we'd be looking at one of three options: another drawbridge, a high bridge with a long approach, or bypassing Everett Station with an inland route.

Assuming we have reached Marysville in a timely manner, the current section from Marysville to just south of Bellingham is already the fastest portion of the route, averaging 55 mph after including the two stops in Stanwood and Mount Vernon. For much of this current corridor, Cascades travels near its legal maximum of 79 mph. So for this middle third of the trip we are stuck with a conflict: building new right-of-way is cheapest where the marginal gain is lowest.

Put another way, when thinking about this corridor we have to decide where our priorities lie. Do we make the fast parts faster? Do we make the slow parts less slow? Or would we go all in and do both?

An illustration: imagine you own two cars, a Hummer that gets 10 miles per gallon (mpg) and a Corolla that gets 30mpg. A new hybrid called the Sakura comes on the market that achieves 200mpg. Which saves more fuel, switching the Corolla to a Sakura, or switching the Hummer to a Corolla?

We all intuitively want to go for the highest mileage vehicle, but in this case it would be the worse choice. Over a typical 10,000 miles of driving, the Hummer would use 1,000 gallons, the Corolla would use 333, and the Sakura would use 50. So upgrading the guzzler saves 2.5 times more - 667 gallons! - than improving the economy car even further (283 gallons). This is the simple function f(x)=1/x, where x provides diminishing returns the higher it goes.

Apply this lesson to a high speed rail corridor, and you get some interesting results. The current corridor is 157 miles and takes 4 hours, for an average speed of 39 miles per hour (mph). As high-level examples, let's look at what would happen if we made the fast parts faster, the slow parts less slow, and built an entirely new corridor from scratch.

Make the Fast Parts Faster

Let's imagine that the constraints leading into Seattle and Vancouver prove insurmountable, and we decide to retain the current right-of-way. British Columbia doesn't bring any money to the table. Trains continue to hug the Puget Sound shoreline south of Everett, and they still creak across the Fraser River in New Westminster.

But between Everett and Bellingham, we decide to build a world-class, 240mph corridor, much like California High Speed Rail's "Initial Operating Segment" between Madera and Bakersfield. We buy off every farmer along the way, and we run elevated tracks in the straightest possible alignment. We tunnel under Chuckanut Mountain to reach a station in Downtown Bellingham. What kind of corridor would we have?

The first 34 miles from Seattle to Everett would still take 52 minutes, and the last 62 miles into Vancouver would still take 1 hour and 48 minutes. But we would build 56 miles of 240mph high-speed track, giving us a magical 15-20 minute running time between Everett and Bellingham. Assuming $100m/mile for rural HSR and another $2B for a Chuckanut Mountain tunnel, we would spend $7B to shave an hour off the trip.

Cost: $7 Billion
Travel Time: 3 Hours

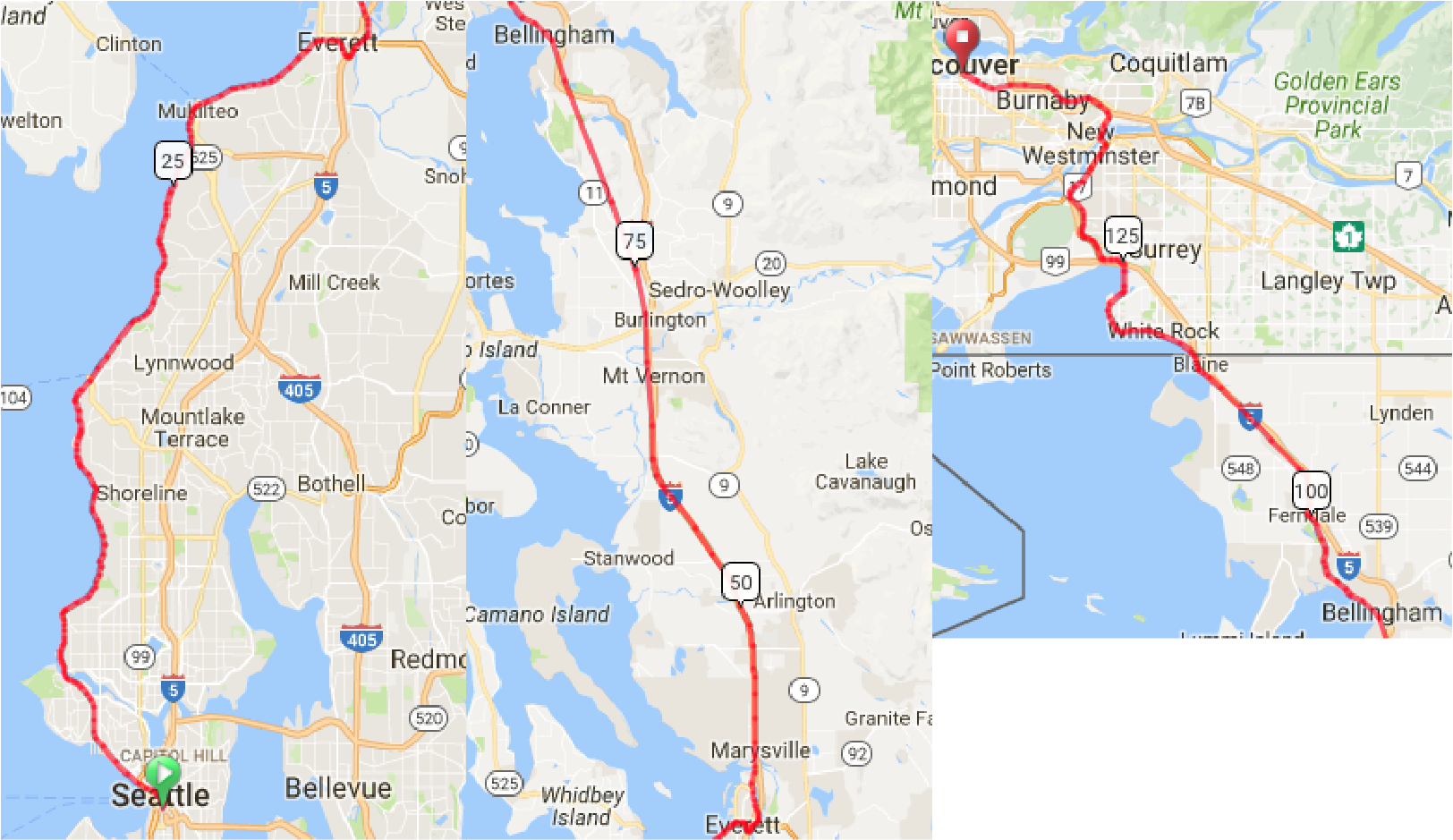
Current Right-of-Way Seattle to Everett and Bellingham-Vancouver
New 240mph Track Everett to Bellingham

Make the Slow Parts Less Slow

Now imagine we took the opposite approach, retaining our current 79mph track between Everett and Samish. Instead, we pour all our money into building a modest 120mph HSR right-of-way from Seattle to Everett and from Bellingham to Vancouver:

• Seattle to Everett, 28 miles, 14 minutes, 120 mph
• Everett to Bellingham, 61 miles, 81 minutes, 45 mph
• Bellingham to Vancouver, 50 miles, 25 minutes, 120 mph

If we assume the last 25 miles into each city cost $500m/mile, and 28 miles of new rural track at $100m/mile, we get:

Cost: $28 Billion
Travel Time: 2 Hours

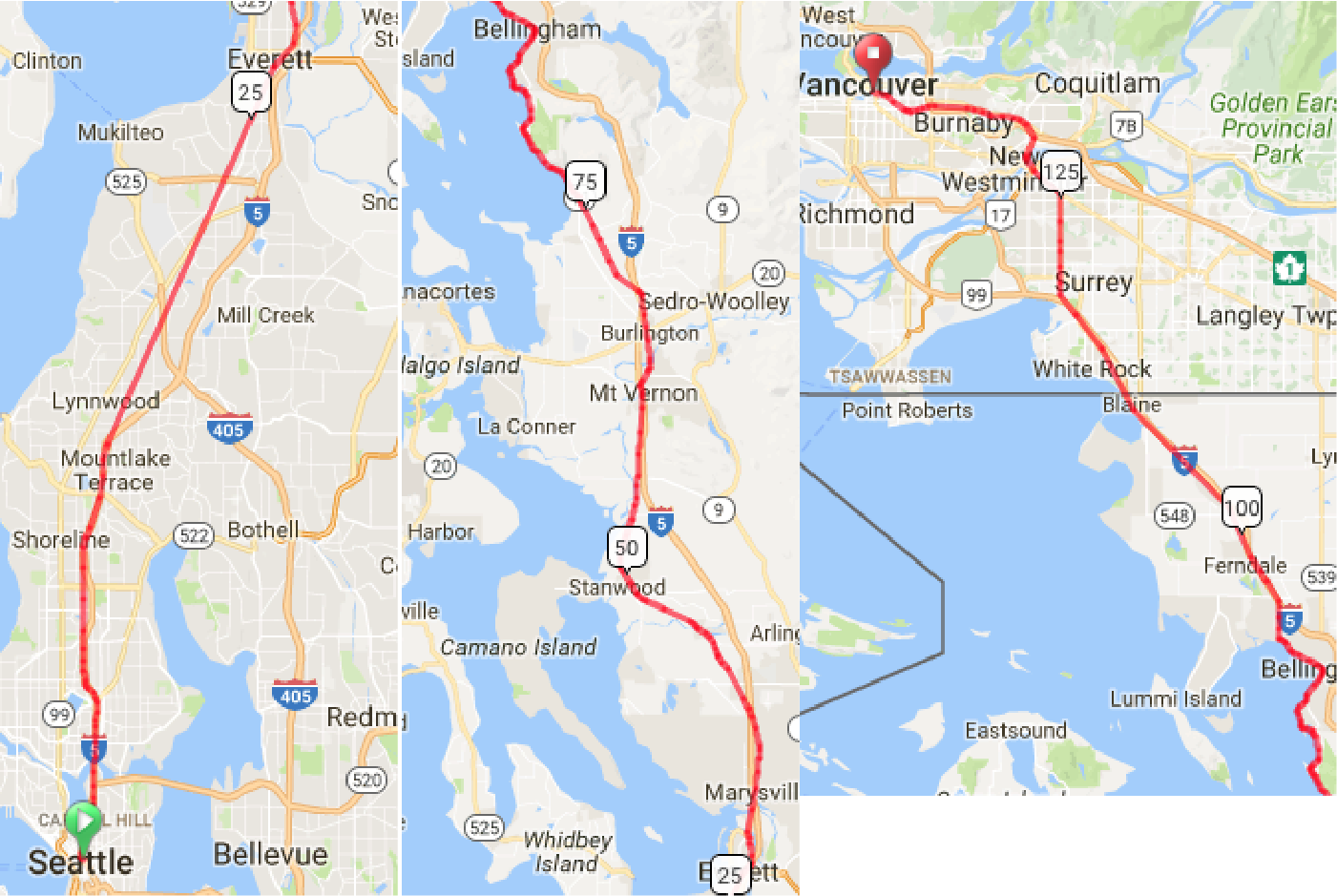
New Right-of-Way (ROW) Approaching Seattle and Vancouver. Improved current ROW between Everett and Bellingham.

Build a New Corridor from Scratch

Now let's go all out. 50 miles of urban track at $500m/mile. 100 miles of rural track at $100m/mile. Two tunnels, in South Everett and at Chuckanut Mountain, at $2B each. New bridges across the Snohomish, Skagit, and Fraser Rivers, at $500m each. Track speeds are 240mph, with an average speed of 180mph after stops in Everett and Bellingham. We get:

Cost: $41 Billion
Travel Time: 45-50 minutes

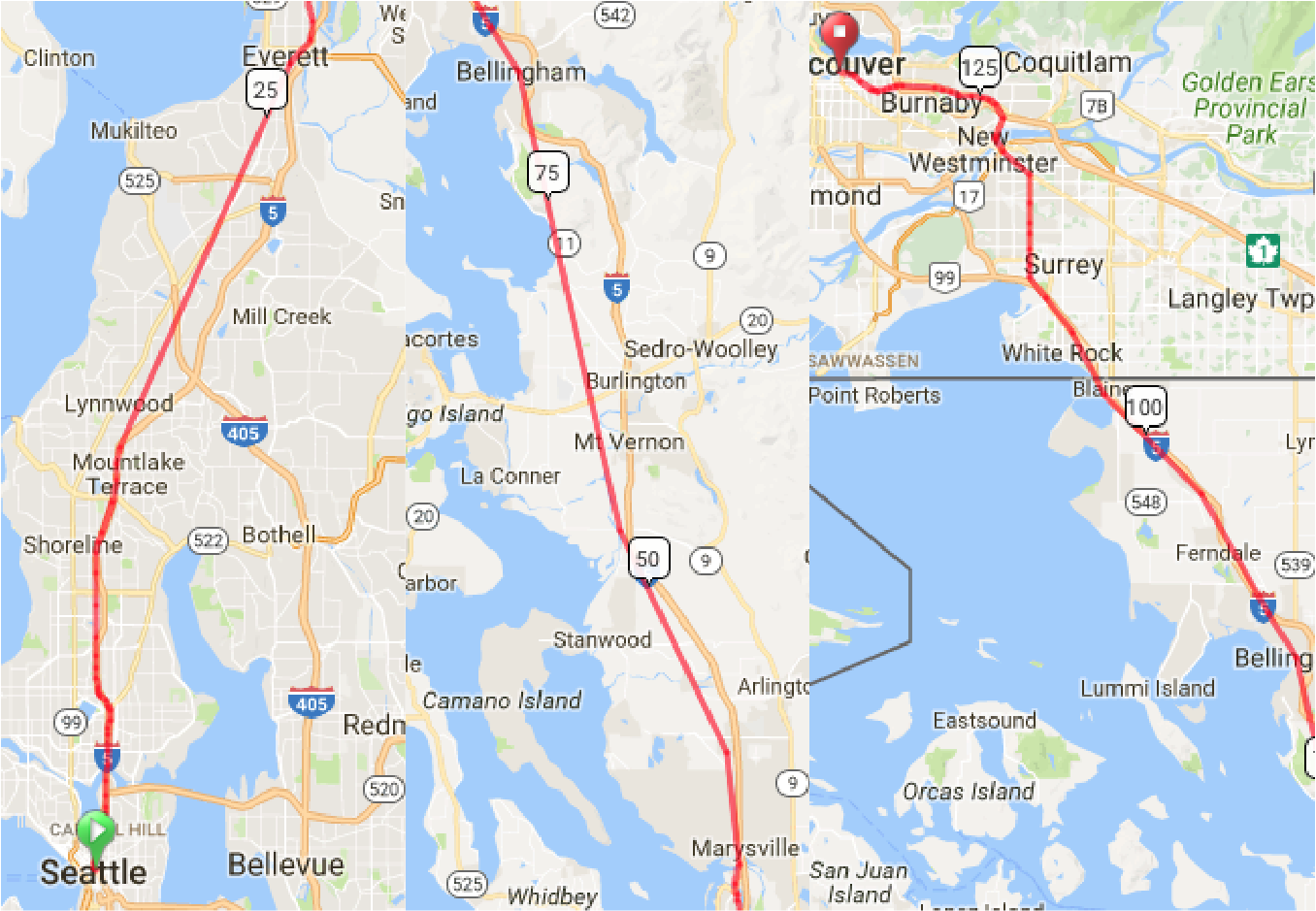
New Corridor Using I-5 Express Lanes, Northgate-Shoreline I-5 Bypass, Tunnel from South Everett to Everett, new elevated Right-of-Way from Marysville to Samish, a Chuckanut Mountain Tunnel, White Rock Bypass, Elevated Running in Residential Surrey, and Improved Current Alignment from New Westminster to Vancouver

Conclusions

The above illustrations are not alignment proposals, but typologies for prioritization of capital resources. There are an infinite number of other combinations, including spot fixes at the slowest spots throughout the entire corridor, suburban terminals (Lynnwood to Scott Road Skytrain?), etc etc.

The broader points to think about are philosophical and political, such as the diminishing returns at higher speed increments and the differential costs of urban and rural construction. Certain benefits are only unlocked at higher speeds and/or with new ROW, such as electrification, lighter rolling stock, and much higher frequency by completely avoiding freight conflicts. The utility to speed ratio is also not linear, as there is likely a threshold speed at which day trips become realistically feasible. At 4 hours each way, it's an overnight. At less than 2 hours, it's a business day trip. At less than an hour, it's a realistic commute. Exponential cost curve, exponential utility.

There is no current demand for such a high-speed service, mostly because good service has never existed to induce it. Any development of HSR is inherently speculative rather than responsive to need. But a region of 3 million people is just 150 miles away, and for the most part we ignore each other on a daily basis. If there were HSR, what level of additional integration could we expect, given the closed border? Any success would likely depend on increasing the reciprocity of labor and capital, harmonizing immigration and drug policies, and hoping for a less dysfunctional federal government.

But the idea of Vancouver just a lunch hour away, with a seamless border, and economic synergy between 7 million people? It's tantalizing to say the least.